题目内容
已知点F1(-4,0),F2(4,0),又P(x,y)是曲线 上的点,则( )
上的点,则( )A.|PF1|+|PF2|=10
B.|PF1|+|PF2|<10
C.|PF1|+|PF2|≤10
D.|PF1|+|PF2|≥10
【答案】分析:法一:根据方程 ,可以联想椭圆
,可以联想椭圆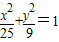 ,根据椭圆的定义可知,
,根据椭圆的定义可知, 是以点F1(-4.0),F2(4,0)为焦点的椭圆,在椭圆上任意取点,可以证明点在曲线
是以点F1(-4.0),F2(4,0)为焦点的椭圆,在椭圆上任意取点,可以证明点在曲线 的内部或在曲线上,即椭圆上的点在封闭曲线的内部或曲线上,故可得结论.
的内部或在曲线上,即椭圆上的点在封闭曲线的内部或曲线上,故可得结论.
法二:任取点P(x,y)在曲线 上,可令
上,可令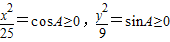 ,A∈[0,
,A∈[0, ],易证得sinA+cosA≥1,即
],易证得sinA+cosA≥1,即 由此知点P(x,y)在
由此知点P(x,y)在 上可其外部,再由椭圆的定义易选出正确选项
上可其外部,再由椭圆的定义易选出正确选项
解答:解:根据方程 ,可以联想椭圆
,可以联想椭圆 ,
,
在椭圆 上取点Q(5cosα,3sinα),即x=5cosα,y=3sinα
上取点Q(5cosα,3sinα),即x=5cosα,y=3sinα
则 =2
=2
∵0≤sin2α≤1,
∴
即点Q在曲线 的内部或在曲线上
的内部或在曲线上
所以椭圆 上的点在封闭曲线
上的点在封闭曲线 的内部或曲线上
的内部或曲线上
由题意, 是以点F1(-4.0),F2(4,0)为焦点的椭圆
是以点F1(-4.0),F2(4,0)为焦点的椭圆
∴当P点恰好取在顶点上时,此时点P在椭圆上,故有|PF1|+|PF2|=10
点P不在曲线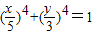 的顶点上时,必有点P在椭圆的外部,故|PF1|+|PF2|>10
的顶点上时,必有点P在椭圆的外部,故|PF1|+|PF2|>10
综上所述,|PF1|+|PF2|≥10
故选D.
法二:任取点P(x,y)在曲线 上,可令
上,可令 ,A∈[0,
,A∈[0, ]
]
则有sinA+cosA≥1,即 由此知点P(x,y)在
由此知点P(x,y)在 上可其外部,故有|PF1|+|PF2|≥10
上可其外部,故有|PF1|+|PF2|≥10
故选D
点评:本题以曲线为载体,考查类比思想,考查椭圆的定义,考查学生分析解决问题的能力.
 ,可以联想椭圆
,可以联想椭圆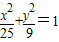 ,根据椭圆的定义可知,
,根据椭圆的定义可知, 是以点F1(-4.0),F2(4,0)为焦点的椭圆,在椭圆上任意取点,可以证明点在曲线
是以点F1(-4.0),F2(4,0)为焦点的椭圆,在椭圆上任意取点,可以证明点在曲线 的内部或在曲线上,即椭圆上的点在封闭曲线的内部或曲线上,故可得结论.
的内部或在曲线上,即椭圆上的点在封闭曲线的内部或曲线上,故可得结论.法二:任取点P(x,y)在曲线
 上,可令
上,可令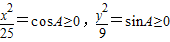 ,A∈[0,
,A∈[0, ],易证得sinA+cosA≥1,即
],易证得sinA+cosA≥1,即 由此知点P(x,y)在
由此知点P(x,y)在 上可其外部,再由椭圆的定义易选出正确选项
上可其外部,再由椭圆的定义易选出正确选项解答:解:根据方程
 ,可以联想椭圆
,可以联想椭圆 ,
,在椭圆
 上取点Q(5cosα,3sinα),即x=5cosα,y=3sinα
上取点Q(5cosα,3sinα),即x=5cosα,y=3sinα则
 =2
=2
∵0≤sin2α≤1,
∴

即点Q在曲线
 的内部或在曲线上
的内部或在曲线上所以椭圆
 上的点在封闭曲线
上的点在封闭曲线 的内部或曲线上
的内部或曲线上由题意,
 是以点F1(-4.0),F2(4,0)为焦点的椭圆
是以点F1(-4.0),F2(4,0)为焦点的椭圆 ∴当P点恰好取在顶点上时,此时点P在椭圆上,故有|PF1|+|PF2|=10
点P不在曲线
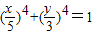 的顶点上时,必有点P在椭圆的外部,故|PF1|+|PF2|>10
的顶点上时,必有点P在椭圆的外部,故|PF1|+|PF2|>10 综上所述,|PF1|+|PF2|≥10
故选D.
法二:任取点P(x,y)在曲线
 上,可令
上,可令 ,A∈[0,
,A∈[0, ]
]则有sinA+cosA≥1,即
 由此知点P(x,y)在
由此知点P(x,y)在 上可其外部,故有|PF1|+|PF2|≥10
上可其外部,故有|PF1|+|PF2|≥10故选D
点评:本题以曲线为载体,考查类比思想,考查椭圆的定义,考查学生分析解决问题的能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 -
- =1
=1 -
- =1(y>0)
=1(y>0) -
- =1或
=1或  -
- =1
=1 -
- =1
=1 -
- =1(x>0)
=1(x>0)