题目内容
已知点F1(-4,0)和F2(4,0),曲线上的动点P到F1、F2的距离之差为6,则曲线方程为( )A.
 -
- =1
=1B.
 -
- =1(y>0)
=1(y>0)C.
 -
- =1或
=1或  -
- =1
=1D.
 -
- =1
=1E.
 -
- =1(x>0)
=1(x>0)
【答案】分析:由于|F1F2|=8>6,利用双曲线的定义即可得到答案.
解答:解:∵F1(-4,0)和F2(4,0),曲线上的动点P到F1、F2的距离之差为6,
即|PF1|-|PF2|=6<|F1F2|=8,
∴由双曲线的定义可知,动点P的轨迹为单支双曲线,2a=6,2c=8,
∴b2=c2-a2=16-9=7,
∴曲线方程为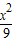 -
-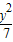 =1(x>0),
=1(x>0),
故选E.
点评:本题考查双曲线的标准方程,掌握双曲线的概念是根本,忽视概念中的“差的绝对值”是易错之处,属于中档题.
解答:解:∵F1(-4,0)和F2(4,0),曲线上的动点P到F1、F2的距离之差为6,
即|PF1|-|PF2|=6<|F1F2|=8,
∴由双曲线的定义可知,动点P的轨迹为单支双曲线,2a=6,2c=8,
∴b2=c2-a2=16-9=7,
∴曲线方程为
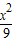 -
-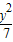 =1(x>0),
=1(x>0),故选E.
点评:本题考查双曲线的标准方程,掌握双曲线的概念是根本,忽视概念中的“差的绝对值”是易错之处,属于中档题.

练习册系列答案
相关题目
 上的点,则( )
上的点,则( )