题目内容
给定公比为 q ( q≠1)的等比数列{ a n},设 b 1=a 1+a 2+a 3,b 2=a 4+a 5+a 6,…,b n=a 3n-2+a 3n-1+a 3n,…,则数列{ b n}
- A.是等差数列
- B.是公比为 q 的等比数列
- C.是公比为 q 3的等比数列
- D.既非等差数列也非等比数列
C
分析:由题意an=a1qn-1,bn=a 3n-2+a 3n-1+a 3n,可得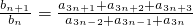 =q3,故数列{bn}是公比为q3的等比数列
=q3,故数列{bn}是公比为q3的等比数列
解答:由题意an=a1qn-1,bn=a 3n-2+a 3n-1+a 3n
∴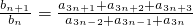 =
=
= =q3
=q3
因此,数列{bn}是公比为q3的等比数列.
故选C.
点评:本题为等比数列的判定,证明数列的后一项与前一项的比值是确定的常数是解决问题的关键,属中档题.
分析:由题意an=a1qn-1,bn=a 3n-2+a 3n-1+a 3n,可得
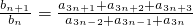 =q3,故数列{bn}是公比为q3的等比数列
=q3,故数列{bn}是公比为q3的等比数列解答:由题意an=a1qn-1,bn=a 3n-2+a 3n-1+a 3n
∴
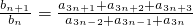 =
=
=
 =q3
=q3因此,数列{bn}是公比为q3的等比数列.
故选C.
点评:本题为等比数列的判定,证明数列的后一项与前一项的比值是确定的常数是解决问题的关键,属中档题.

练习册系列答案
相关题目