Question

已知向量

OB

=(2，0)，

OC

=(2，2)（O为坐标原点），

CA

=(

2

cosα，

2

sinα)，则向量

OA

与

OB

的夹角范围为

 

．

Answer 1

分析：由|

CA

|=

2

，故点A在以点C（2，2）为圆心，以

2

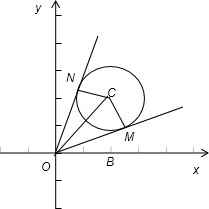
为半径的圆上，如图，故向量

OA

与

OB

的夹角最小为∠MOB，最大为∠NOB，从而得到向量

OA

与

OB

的夹角范围．

解答：解：由|

CA

|=

2

，故点A在以点C（2，2）为圆心，以

2

为半径的圆上，如图：
过原点O，作圆的两条切线OM、ON，则∠COM=

π

6

，又∠COB=

π

4

，∴∠MOB=

π

4

-

π

6

=

π

12

，
∠NOB=

π

4

+

π

6

=

5π

12

． 故向量

OA

与

OB

的夹角最小为∠MOB，最大为∠NOB．
故向量

OA

与

OB

的夹角范围为 [

π

12

，

5

12

π]，故答案为 [

π

12

，

5

12

π]．

点评：本题考查向量的模的定义，向量的模的几何意义，求向量的模的方法，体现了数形结合的数学思想，判断
向量

OA

与

OB

的夹角最小为∠MOB，最大为∠NOB，是解题的关键．