题目内容

已知向量
OB
=(-2，0)， 
OC
=(2，
0)，
CA
=(cosθ，sinθ)
，则cos＜
OA
，
OB
＞的取值范围是（　　）
A、[
15
4
，1]
B、[-
3
2
，1]
C、[-1，
2
5
5
]
D、[-1，-
3
2
]
分析：由已知，在平面直角坐标系中，A点得轨迹是以C为圆心，以1为半径的圆，借助于直线OB与圆C的位置关系求出，
OA
，
OB
夹角范围，再求出余弦值取值范围．
解答：解：
OA
=
OC
+
CA
，在平面直角坐标系中，A点得轨迹是以C为圆心，以1为半径的圆，如图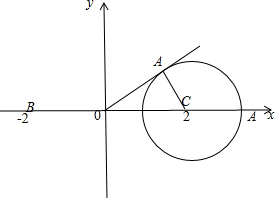精英家教网
当OA与圆C相切时，sin∠AOC=
1
2
，∠AOC=30°，
OA
，
OB
夹角最小为180°-30°=150°
当A在x轴时，
OA
，
OB
夹角最大为180°．根据余弦函数单调性，则cos＜
OA
，
OB
＞的取值范围是 [-1，-
3
2
]
故选D
点评：本题考查向量的夹角运算，采用数形结合的思想方法，更容易解决．
练习册系列答案
相关题目
已知向量
OB
=(2，0)，
OC
=(2，2)，
CA
=(
2
cosθ，
2
sinθ)（θ∈R），则向量
OA
与
OB
的夹角的取值范围是（　　）
A、[
π
12
，
π
3
]
B、[
π
4
，
π
12
]
C、[
π
12
，
5π
12
]
D、[
5π
12
，
π
2
]
已知向量
OB
=(2，0)，
OC
=(2，2)（O为坐标原点），
CA
=(
2
cosα，
2
sinα)，则向量
OA
与
OB
的夹角范围为
 
．
已知向量
OB
=(2，0)，
OC
=(2，2)，
CA
=(
2
cosθ，
2
sinθ)，α为
OA
与
OB
的夹角，则α的取值范围是
[
π
12
，
5π
12
]
[
π
12
，
5π
12
]
．
已知向量
OB
=(2，0)，
OC
=(0，2)，
CA
=(
3
cosθ，
3
sinθ)，则
OA
与
OB
夹角的范围是
[
π
6
，
5π
6
]
[
π
6
，
5π
6
]
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网