题目内容

设函数f（x）=x|x|+bx+c，给出下列命题：①b=0，c＞0时，方程f（x）=0只有一个实数根；②c=0时，y=f（x）是奇函数；③方程f（x）=0至多有两个实根．上述三个命题中所有正确命题的序号为
 
．
分析：根据题意，依次分析三个命题，①b=0，c＞0时，f（x）=x|x|+c=
x2+c (x≥0)
-x2+c (x＜0)
，如图①，结合图形作答．
②c=0时，f（x）=x|x|+bx，显然是奇函数，③当c=0，b＜0时，如图②，f（x）=x|x|+bx=
x2+bx (x≥0)
-x2+bx (x＜0)
，结合图形作答．
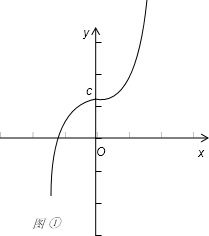
解答：解：①b=0，c＞0时，f（x）=x|x|+c=
x2+c (x≥0)
-x2+c (x＜0)
，如图①，曲线与x轴只有一个交点，
所以方程f（x）=0 只有一个实数根，正确．
②c=0时，f（x）=x|x|+bx，显然是奇函数．
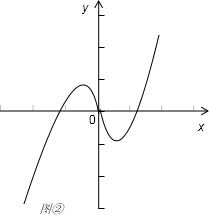
③当c=0，b＜0时，如图②，f（x）=x|x|+bx=
x2+bx (x≥0)
-x2+bx (x＜0)
，
方程f（x）=0可以有三个实数根．
综上所述，正确命题的序号为①②．
精英家教网精英家教网
点评：本题考查函数的奇偶性，方程根的个数判断，体现了数形结合的数学思想．
练习册系列答案
相关题目
设函数f（x）=a2x2（a＞0），g（x）=blnx．
（1）若函数y=f（x）图象上的点到直线x-y-3=0距离的最小值为
2
，求a的值；
（2）关于x的不等式（x-1）2＞f（x）的解集中的整数恰有3个，求实数a的取值范围；
（3）对于函数f（x）与g（x）定义域上的任意实数x，若存在常数k，m，使得f（x）≥kx+m和g（x）≤kx+m都成立，则称直线y=kx+m为函数f（x）与g（x）的“分界线”．设a=
2
2
，b=e，试探究f（x）与g（x）是否存在“分界线”？若存在，求出“分界线”的方程；若不存在，请说明理由．
设函数f（x）的定义域为A，若存在非零实数t，使得对于任意x∈C（C⊆A），有x+t∈A，且f（x+t）≤f（x），则称f（x）为C上的t低调函数．如果定义域为[0，+∞）的函数f（x）=-|x-m2|+m2，且 f（x）为[0，+∞）上的10低调函数，那么实数m的取值范围是（　　）
A、[-5，5]
B、[-
5
，
5
]
C、[-
10
，
10
]
D、[-
5
2
，
5
2
]
（2012•深圳一模）已知函数f(x)=
1
3
x3+bx2+cx+d，设曲线y=f（x）在与x轴交点处的切线为y=4x-12，f′（x）为f（x）的导函数，且满足f′（2-x）=f′（x）．
（1）求f（x）；
（2）设g(x)=x
f′(x)
 ， m＞0，求函数g（x）在[0，m]上的最大值；
（3）设h（x）=lnf′（x），若对一切x∈[0，1]，不等式h（x+1-t）＜h（2x+2）恒成立，求实数t的取值范围．
设函数f（x）是定义在R上的偶函数，且f（x+2）=f（x）恒成立；当x∈[0，1]时，f（x）=x3-4x+3．有下列命题：
①f(-
3
4
) ＜f(
15
2
)；
②当x∈[-1，0]时f（x）=x3+4x+3；
③f（x）（x≥0）的图象与x轴的交点的横坐标由小到大构成一个无穷等差数列；
④关于x的方程f（x）=|x|在x∈[-3，4]上有7个不同的根．
其中真命题的个数为（　　）
设函数f（x）=a2x2（a＞0），g（x）=blnx．
（1）若函数y=f（x）图象上的点到直线x-y-3=0距离的最小值为2
2
，求a的值；
（2）关于x的不等式（x-1）2＞f（x）的解集中的整数恰有3个，求实数a的取值范围；
（3）对于函数f（x）与g（x）定义域上的任意实数x，若存在常数k，m，使得f（x）≥kx+m和g（x）≤kx+m都成立，则称直线y=kx+m为函数f（x）与g（x）的“分界线”．设a=
2
2
，b=e，试探究f（x）与g（x）是否存在“分界线”？若存在，求出“分界线”的方程；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网