题目内容
已知a>0,定义在D上的函数f(x)和g(x)的值域依次是[-(2a+3)π3,a+6]和[a2+
,(a2+
)π4],若存在x1,x2∈D,使得|f(x1)-g(x2)|<
成立,则a的取值范围为
| 25 |
| 4 |
| 25 |
| 4 |
| 1 |
| 4 |
(0,1)
(0,1)
.分析:定义在D上的函数f(x)和g(x)的值域,得到:f(x)的最大值为a+6,g(x)的最小值为:a2+
,结合条件:存在x1,x2∈D,使得|f(x1)-g(x2)|<
成立,得到f(x)的最大值与g(x)的最小值差的绝对值小于
,得出一个关于a的不等关系,|解之即得a的取值范围.
| 25 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
解答:解:∵定义在D上的函数f(x)和g(x)的值域依次是[-(2a+3)π3,a+6]和[a2+
,(a2+
)π4],
∴f(x)的最大值为a+6,g(x)的最小值为:a2+
,
∵存在x1,x2∈D,使得|f(x1)-g(x2)|<
成立,则
∴|a2+
-(a+6)|<
,
解之得:0<a<1,
故答案为:(0,1).
| 25 |
| 4 |
| 25 |
| 4 |
∴f(x)的最大值为a+6,g(x)的最小值为:a2+
| 25 |
| 4 |
∵存在x1,x2∈D,使得|f(x1)-g(x2)|<
| 1 |
| 4 |
∴|a2+
| 25 |
| 4 |
| 1 |
| 4 |
解之得:0<a<1,
故答案为:(0,1).
点评:本小题主要考查函数的值域、函数的最值的应用、不等式的解法等基础知识,考查运算求解能力,考查化归与转化思想.属于中档题.

练习册系列答案
相关题目
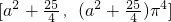 ,若存在
,若存在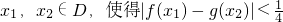 成立,则a的取值范围为________.
成立,则a的取值范围为________.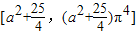 ,若存在
,若存在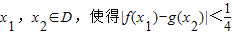 成立,则a的取值范围为 .
成立,则a的取值范围为 . ,若存在x1,x2∈D,使得
,若存在x1,x2∈D,使得 成立,则a的取值范围为( )。
成立,则a的取值范围为( )。