题目内容
2. 长方体ABCD-A1B1C1D1中,AB=BC=2a,AA1=a,E和F分别是A1B1和BB1的中点,求:
长方体ABCD-A1B1C1D1中,AB=BC=2a,AA1=a,E和F分别是A1B1和BB1的中点,求:(1)EF和AD1所成角的正弦值;
(2)AC1和B1C所成角的余弦值.
分析 (1)由EF∥A1B,AD1∥BC1,得∠A1BC1是EF和AD1所成角,由此利用余弦定理能求出EF和AD1所成角的正弦值.
(2)延长D1A1到F使A1F=D1A1,则AF∥DA1∥CB1,从而AC1和B1C所成角为AF与AC1的夹角,由此利用余弦定理能求出AC1与B1C所成角的余弦值.
解答 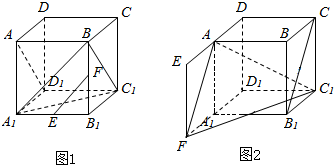 解:(1)如图1,∵EF∥A1B,AD1∥BC1,
解:(1)如图1,∵EF∥A1B,AD1∥BC1,
∴∠A1BC1是EF和AD1所成角,
∵长方体ABCD-A1B1C1D1中,AB=BC=2a,AA1=a,E和F分别是A1B1和BB1的中点,
∴AD1=$\sqrt{{a}^{2}+4{a}^{2}}$=$\sqrt{5}$a=BC1,A1B=$\sqrt{{a}^{2}+4{a}^{2}}$=$\sqrt{5}$a,
A1C1=$\sqrt{4{a}^{2}+4{a}^{2}}$=2$\sqrt{2}$a,
∴cos∠A1BC1=$\frac{5{a}^{2}+5{a}^{2}-8{a}^{2}}{2×5{a}^{2}}$=$\frac{1}{5}$,
∴sin∠A1BC1=$\sqrt{1-(\frac{1}{5})^{2}}$=$\frac{2\sqrt{6}}{5}$.
(2)如图2,延长D1A1到F使A1F=D1A1,则AF∥DA1∥CB1,
∴AC1和B1C所成角为AF与AC1的夹角,即∠FAC1(或其补角),
∵AF=B1C=$\sqrt{5}$a,AC1=$\sqrt{{a}^{2}+4{a}^{2}+4{a}^{2}}$=3a,
FC1=$\sqrt{(2a)^{2}+(4a)^{2}}$=2$\sqrt{5}$a,
∴cos∠FAC1=$\frac{5{a}^{2}+9{a}^{2}-20{a}^{2}}{2×\sqrt{5}a×3a}$=$\frac{-6}{6\sqrt{5}}$=-$\frac{\sqrt{5}}{5}$,
∴AC1与B1C所成角的余弦值为$\frac{\sqrt{5}}{5}$.
点评 本题考查异面直线所成角的正弦值和余弦值的求法,是中档题,解题时要认真审题,注意余弦定理的合理运用.

 科学实验活动册系列答案
科学实验活动册系列答案| A. | $\frac{5}{6}$ | B. | -$\frac{5}{6}$ | C. | $\frac{6}{5}$ | D. | -$\frac{6}{5}$ |
| A. | -$\frac{1}{5}$+$\frac{3}{5}$i | B. | $\frac{1}{5}$+$\frac{3}{5}$i | C. | $\frac{1}{5}$-$\frac{3}{5}$i | D. | -$\frac{1}{5}$-$\frac{3}{5}$i |
| A. | a+b>0 | B. | a+b<0 | C. | a+b=0 | D. | 不确定 |