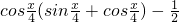题目内容
设函数y=f(x)满足对任意的实数t,都有f(1+t)=-f(1-t),f(t-2)=f(2-t)成立,则下面关于函数y=f(x)的说法:①图象关于点(1,0)对称;②图象关于y轴对称;③以2为周期;④f(2009)=0.其中正确的有
①②④
①②④
(将你认为正确说法前面的序号都填上).分析:利用函数的基本性质,对称中心,周期,分别对选项验证,判定正误即可.
解答:解:①f(1+t)=-f(1-t)恒成立,则函数y=f(x)的图象关于(1,0)点对称;①正确.
②由f(t-2)=f(2-t)⇒f(x)=f(-x),则函数y=f(x)是偶函数,它的图象关于y轴对称,故②正确.
③若f(1+t)=-f(1-t),且f(1-t)=f(t-1)恒成立,⇒f(1+t)=-f(t-1)⇒f(t+2)=-f(t),从而f(t+4)=-f(t+2)=f(t),则函数y=f(x)以4为周期.③错误.
④∵函数y=f(x)以4为周期,∴f(2009)=f(4×502+1)=f(1),
在f(1+t)=-f(1-t)中令t=0得f(1)=-f(1),∴f(1)=0,
∴f(2009)=0.④正确.
故答案为:①②④..
②由f(t-2)=f(2-t)⇒f(x)=f(-x),则函数y=f(x)是偶函数,它的图象关于y轴对称,故②正确.
③若f(1+t)=-f(1-t),且f(1-t)=f(t-1)恒成立,⇒f(1+t)=-f(t-1)⇒f(t+2)=-f(t),从而f(t+4)=-f(t+2)=f(t),则函数y=f(x)以4为周期.③错误.
④∵函数y=f(x)以4为周期,∴f(2009)=f(4×502+1)=f(1),
在f(1+t)=-f(1-t)中令t=0得f(1)=-f(1),∴f(1)=0,
∴f(2009)=0.④正确.
故答案为:①②④..
点评:本题考查函数图象的对称性,函数的周期性,考查学生灵活运用知识的能力,是基础题.

练习册系列答案
相关题目