题目内容
定义运算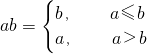
已知函数f（x）=x2⊕x，求f（2）=______．
解：定义运算，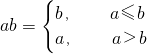
所以函数f（x）=x2⊕x，
若x2≤x，即0≤x≤1，可得f（x）=x，
若x2＞x，即x＞1，可得f（x）=x2，
∴f（2）=22=4，
故答案为4；
分析：已知定义运算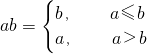，理解其中的含义，就是求最大值，根据新定义求出函数f（x）=x2⊕x的分段函数的解析式，再代入x=2，求出f（2）；
点评：此题考查新定义的运算，实质是考查分段函数的性质及其应用，分段函数代入求值，要注意其定义域，此题是一道基础题；
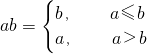，所以函数f（x）=x2⊕x，
若x2≤x，即0≤x≤1，可得f（x）=x，
若x2＞x，即x＞1，可得f（x）=x2，
∴f（2）=22=4，
故答案为4；
分析：已知定义运算
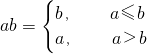，理解其中的含义，就是求最大值，根据新定义求出函数f（x）=x2⊕x的分段函数的解析式，再代入x=2，求出f（2）；点评：此题考查新定义的运算，实质是考查分段函数的性质及其应用，分段函数代入求值，要注意其定义域，此题是一道基础题；
练习册系列答案
相关题目
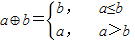已知函数f（x）=x2⊕x，求f（2）= ．
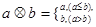已知函数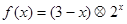
则f(x)的 最大值为_________