题目内容
当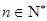 时,
时,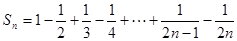
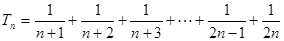
(1)求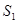 ,
,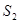 ,
,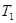 ,
,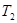 ;
;
(2)猜想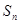 与
与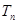 的关系,并用数学归纳法证明.
的关系,并用数学归纳法证明.
【答案】
(1)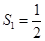 ,
,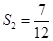
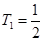
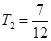
(2)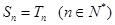 证明见解析
证明见解析
【解析】(1)分别令n=1,n=2可求出S1,S2,T1,T2.
(2)根据(I)当中的结果,猜想出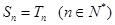 ,
,
因为是与正整数n有关的等式可以考虑采用数学归纳法证明.
再证明时一定要按两个步骤进行,缺一不可.
第一步,先验证:n=1时等式成立.
第二步,先假设n=k时,等式成立;再证明n=k+1时,等式也成立,但必须要用上n=k时,归纳假设,否则证明无效
(1)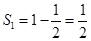 ,
,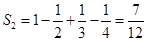
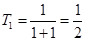
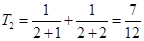 ………4分
………4分
(2)猜想: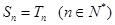 即:
即:
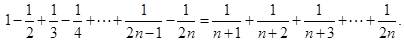 (n∈N*)6分
(n∈N*)6分
下面用数学归纳法证明
① n=1时,已证S1=T1 ………………7分
② 假设n=k时,Sk=Tk(k≥1,k∈N*),即:
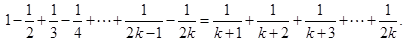 ……………9分
……………9分
则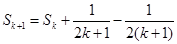
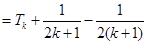 …11分
…11分

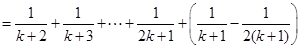
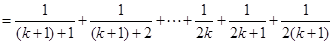
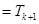
由①,②可知,对任意n∈N*,Sn=Tn都成立.

练习册系列答案
相关题目
 满足:当
满足:当 时,
时, ,
,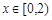 时,
时,
 时,
时, 的表达式;
的表达式; 满足什么条件时,函数
满足什么条件时,函数 有4个零点,
有4个零点, 满足:当
满足:当 时,
时, ,当
,当 时,
时,
 时,
时, 的表达式;
的表达式; 与函数
与函数 的图象恰好有两个公共点,求实数
的图象恰好有两个公共点,求实数 的取值范围。
的取值范围。 满足什么条件时,函数
满足什么条件时,函数 有4个零点且这4个零点从小到大依次成等差数列。
有4个零点且这4个零点从小到大依次成等差数列。 是定义在
是定义在 上的奇函数,当
上的奇函数,当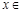
 时,
时, .
.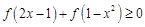 .
.