题目内容
设函数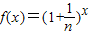 (n∈N,且n>1,x∈N).
(n∈N,且n>1,x∈N).(Ⅰ)当x=6时,求
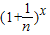 的展开式中二项式系数最大的项;
的展开式中二项式系数最大的项;(Ⅱ)对任意的实数x,证明
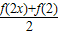 >f'(x)(f'(x)是f(x)的导函数);
>f'(x)(f'(x)是f(x)的导函数);(Ⅲ)是否存在a∈N,使得an<
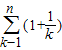 <(a+1)n恒成立?若存在,试证明你的结论并求出a的值;若不存在,请说明理由.
<(a+1)n恒成立?若存在,试证明你的结论并求出a的值;若不存在,请说明理由.
【答案】分析:(1)利用二项式系数的特点,找到展开式系数最大的项,即第四项;
(2)利用基本不等式适当放缩进行证明或函数思想进行转化与证明;
(3)探究性问题处理不等式问题,要注意对展开式系数进行适当放缩从而达到证明的目的.
解答:解:(Ⅰ)展开式中二项式系数最大的项是第4项,这项是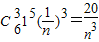
(Ⅱ)证法一:因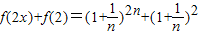
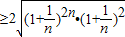 =
=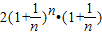
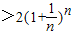
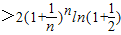
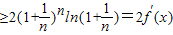
证法二:因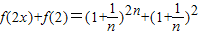
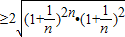 =
=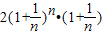
而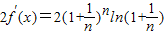
故只需对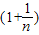 和
和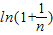 进行比较.
进行比较.
令g(x)=x-lnx(x≥1),有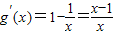
由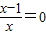 ,得x=1
,得x=1
因为当0<x<1时,g′(x)<0,g(x)单调递减;当1<x<+∞时,g′(x)>0,g(x)单调递增,所以在x=1处g(x)有极小值1
故当x>1时,g(x)>g(1)=1,
从而有x-lnx>1,亦即x>lnx+1>lnx
故有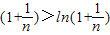 恒成立.
恒成立.
所以f(2x)+f(2)≥2f′(x),原不等式成立.
(Ⅲ)对m∈N,且m>1
有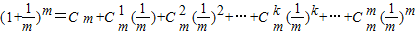
=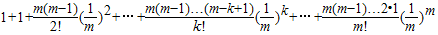
=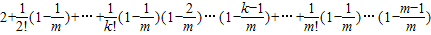
<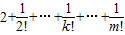
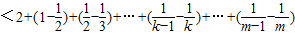
=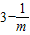
<3;
又因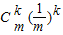 >0(k=2,3,…,m),故
>0(k=2,3,…,m),故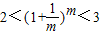
∵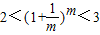 ,从而有
,从而有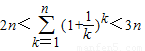 成立,
成立,
即存在a=2,使得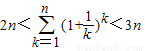 恒成立.
恒成立.
点评:本题考查函数、不等式、导数、二项式定理、组合数计算公式等内容和数学思想方法.考查综合推理论证与分析解决问题的能力及创新意识.
(2)利用基本不等式适当放缩进行证明或函数思想进行转化与证明;
(3)探究性问题处理不等式问题,要注意对展开式系数进行适当放缩从而达到证明的目的.
解答:解:(Ⅰ)展开式中二项式系数最大的项是第4项,这项是
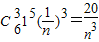
(Ⅱ)证法一:因
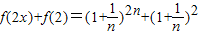
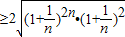 =
=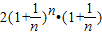
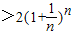
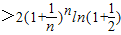
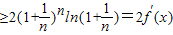
证法二:因
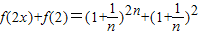
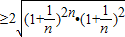 =
=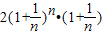
而
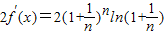
故只需对
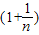 和
和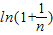 进行比较.
进行比较.令g(x)=x-lnx(x≥1),有
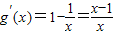
由
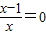 ,得x=1
,得x=1因为当0<x<1时,g′(x)<0,g(x)单调递减;当1<x<+∞时,g′(x)>0,g(x)单调递增,所以在x=1处g(x)有极小值1
故当x>1时,g(x)>g(1)=1,
从而有x-lnx>1,亦即x>lnx+1>lnx
故有
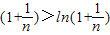 恒成立.
恒成立.所以f(2x)+f(2)≥2f′(x),原不等式成立.
(Ⅲ)对m∈N,且m>1
有
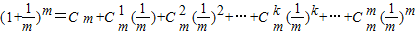
=
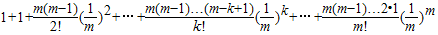
=
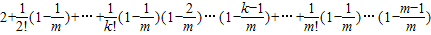
<
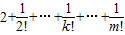
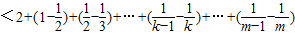
=
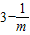
<3;
又因
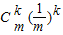 >0(k=2,3,…,m),故
>0(k=2,3,…,m),故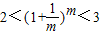
∵
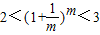 ,从而有
,从而有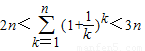 成立,
成立,即存在a=2,使得
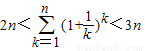 恒成立.
恒成立.点评:本题考查函数、不等式、导数、二项式定理、组合数计算公式等内容和数学思想方法.考查综合推理论证与分析解决问题的能力及创新意识.

练习册系列答案
相关题目
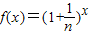 (n∈N,且n>1,x∈N).
(n∈N,且n>1,x∈N).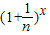 的展开式中二项式系数最大的项;
的展开式中二项式系数最大的项;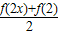 >f'(x)(f'(x)是f(x)的导函数);
>f'(x)(f'(x)是f(x)的导函数);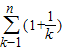 <(a+1)n恒成立?若存在,试证明你的结论并求出a的值;若不存在,请说明理由.
<(a+1)n恒成立?若存在,试证明你的结论并求出a的值;若不存在,请说明理由.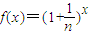 (n∈N,且n>1,x∈N).
(n∈N,且n>1,x∈N).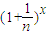 的展开式中二项式系数最大的项;
的展开式中二项式系数最大的项;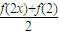 >f'(x)(f'(x)是f(x)的导函数);
>f'(x)(f'(x)是f(x)的导函数);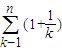 <(a+1)n恒成立?若存在,试证明你的结论并求出a的值;若不存在,请说明理由.
<(a+1)n恒成立?若存在,试证明你的结论并求出a的值;若不存在,请说明理由.