题目内容
【题目】设函数f（x）=Asin（ωx+φ）（A，ω＞0，0＜|φ|＜π）在一个周期内的图象如图所示．
（1）求函数f（x）的解析式；
（2）求g（x）=f（3x+
）﹣1在[﹣
， 
]上的值域．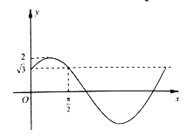
【答案】解：（1）由图形可得：A=2，…2分
将点（0，
），（
，）代入，有φ
，
∵0＜|φ|＜π，
∴
，
故f（x）=2sin（
+
）．
（2）g（x）=f（3x+
）﹣1=2sin[
（3x+）+]﹣1
=2sin（2x+）﹣1=2cos2x﹣1，
当x∈[﹣
，]时，2x∈[﹣，
]，cos2x∈[﹣
，1]，
故g（x）=f（3x+）﹣1在∈[﹣，]上的值域为：[﹣2，1]
【解析】（1）由函数的图象的顶点坐标求出A，由特殊点的坐标求出φ的值，再根据五点法作图求出ω的值，从而求得该函数的解析式．
（2）利用三角函数恒等变换的应用先求函数解析式g（x）=2cos2x﹣1，由x∈[﹣ ， ]，利用余弦函数的图形和性质即可得解其值域．
练习册系列答案
名校课堂系列答案
相关题目
