题目内容
15.设P是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)上一点,F1(-c,0),F2(c,0)(c>0)为左、右焦点,△PF1F2周长为6c,面积$\frac{2\sqrt{3}}{3}$a2,则双曲线的离心率是$\frac{2\sqrt{3}}{3}$.分析 不妨设P在右支上,由双曲线的定义可得PF1-PF2=2a,再由条件分别求得△PF1F2三边长,运用三角形的海伦面积公式,结合离心率公式,解方程即可得到所求值
解答 解:不妨设P在右支上,则PF1-PF2=2a,
又PF1+PF2+F1F2=6c,即PF1+PF2=4c,
解得PF1=a+2c,PF2=2c-a,
由海伦面积公式可得,△PF1F2的面积为
S△=$\sqrt{3c(3c-2c)(3c-a-2c)(3c-2c+a)}$=$\sqrt{3{c}^{2}({c}^{2}-{a}^{2})}$,
由题意可得$\frac{2\sqrt{3}}{3}$a2=$\sqrt{3{c}^{2}({c}^{2}-{a}^{2})}$,
两边平方可得,9c4-9a2c2-4a4=0,
由e=$\frac{c}{a}$,可得,9e4-9e2-4=0,
解得e2=$\frac{4}{3}$,即有e=$\frac{2\sqrt{3}}{3}$.
故答案为:$\frac{2\sqrt{3}}{3}$.
点评 本题考查双曲线的定义、方程和性质,主要考查离心率的求法,同时考查三角形的面积公式的运用,属于中档题.

练习册系列答案
相关题目
6.高二(6)班班主任对全班50名学生进行了有关作业量多少的调查,得到如下列联表:
认为“喜欢玩电脑游戏与认为作业多有关系”的概率有多大?
| 认为作业多 | 认为作业不多 | |
| 喜欢玩电脑游戏 | 18 | 9 |
| 不喜欢玩电脑游戏 | 8 | 15 |
4.双曲线$\frac{{x}^{2}}{9}-\frac{{y}^{2}}{16}$=-1的焦点坐标为( )
| A. | (±3,0) | B. | (±5,0) | C. | (0,±5) | D. | (0,±$\sqrt{7}$) |
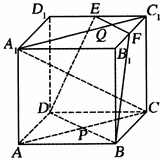 如图:在正方体ABCD-A1B1C1D1中,E,F分别为D1C1,B1C1的中点,AC∩BD=P,A1C1∩EF=Q,直线A1C与平面BDEF的交点为R.
如图:在正方体ABCD-A1B1C1D1中,E,F分别为D1C1,B1C1的中点,AC∩BD=P,A1C1∩EF=Q,直线A1C与平面BDEF的交点为R.