题目内容
12.若函数f(x)是定义在R上的奇函数,则函数F(x)=|f(x)|+f(|x|)的图象一定关于( )| A. | x轴对称 | B. | y轴对称 | C. | 原点对称 | D. | 直线y=x对称 |
分析 根据函数奇偶性的定义和性质进行判断即可.
解答 解:∵函数f(x)是定义在R上的奇函数,
∴F(-x)=|f(-x)|+f(|-x|)=|-f(x)|+f(|x|)=|f(x)|+f(|x|)=F(x),
即函数F(x)是偶函数,则图象关于y轴对称,
故选:B
点评 本题主要考查函数图象的判断,根据函数奇偶性的性质是解决本题的关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
7.计算:log225•log52$\sqrt{2}$=( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
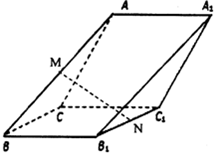 如图,在斜三棱柱ABCD-A1B1C1中,侧面ACC1A1与侧面CBB1C1都是菱形,∠B1C1C=∠C1CA=60°,AC=2,其中M,N分别是AB,B1C1的中点,
如图,在斜三棱柱ABCD-A1B1C1中,侧面ACC1A1与侧面CBB1C1都是菱形,∠B1C1C=∠C1CA=60°,AC=2,其中M,N分别是AB,B1C1的中点,