题目内容

8．在等差数列{an}中，若a1+a2+a3=32，a11+a12+a13=118，则a4+a10=（　　）
A．45B．50C．75D．60

分析 根据等差数列的性质，结合已知，可得a2+a12=50，进而得到a4+a10的值．

解答 解：∵a1+a2+a3=3a2=32，a11+a12+a13=3a12=118，
∴3（a2+a12）=150，
即a2+a12=50，
∴a4+a10=a2+a12=50．
故选：B．

点评 本题考查的知识点是等差数列的性质：若m+n=p+q，则am+an=ap+aq．

练习册系列答案
相关题目
18．已知复数z1=1-i，z1z2=1+i，则z2=（　　）
A．iB．-iC．1+iD．1-i
19．7个人排成一排，在下列情况下，各有多少种不同排法？：
（1）甲不排头，也不排尾：
（2）甲、乙之间有且只有两人：
（3）甲不排头，乙不排当中．
16．设f（x）=|x-a|+2x其中a＞0
（1）当a=2时，求解f（x）≥2x+1
（2）若f（x）≤0的解集为{x|x≤-1}，求a的值．
3．-885°化成2kπ+α（0≤α≤2π，k∈Z）的形式是-6π+$\frac{13π}{12}$．
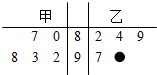13．下面茎叶图是甲、乙两人在5次综合测评中成绩（所有成绩取整数）的茎叶图，其中一个数字被污损，则甲的平均成绩超过乙的平均成绩的概率为$\frac{4}{5}$．
20．（1）若（x+$\frac{1}{x}$）n开式中第3项和第7项的二项式系数相等，求展开式中x-2系数．
（2）若将函数f（x）=x5表示为f（x）=a0+a1（1+x）+a2（1+x）2+…+a5（1+x）5，求a3．
（3）已知（x+$\frac{a}{x}$）（2x-$\frac{1}{x}$）5的展开式中各项系数的和为2，求该展开式中x2的系数．
17．已知定义在R上的函数f（x）=ax2+2x+3的值域为[2，+∞），则f（x）的单调增区间为[-1，+∞）．
18．不等式组$\left\{\begin{array}{l}{y≥-1}\\{x+y≤4}\\{5x-3y≥0}\end{array}\right.$表示的平面区域的面积是7．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网