题目内容
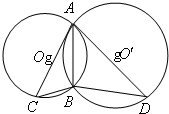（2010•广东模拟）（几何证明选讲）如图，⊙O和⊙O'相交于A，B两点，AC是⊙O'的切线，交⊙O于点C，AD是⊙O的切线，交⊙O'于点D，若BC=2，BD=8，则AB=4
4
．分析：根据题意在△ACB与△ADB中，∠CAB=∠ADB，∠DAB=∠ACB，从而可判断△ACB与△ADB相似，从而有
=
，而BC=2，BD=8，从而可求得AB．
| BC |
| AB |
| AB |
| BD |
解答：解：∵⊙O和⊙O'相交于A，B两点，AC是⊙O'的切线，交⊙O于点C，AD是⊙O的切线，交⊙O'于点D，
∴在△ACB与△ADB中，∠CAB=∠ADB，∠DAB=∠ACB，
∴△ACB∽△ADB，
∴
=
，
又BC=2，BD=8，
∴AB2=2×8=16，∴AB=4．
故答案为：4．
∴在△ACB与△ADB中，∠CAB=∠ADB，∠DAB=∠ACB，
∴△ACB∽△ADB，
∴
| BC |
| AB |
| AB |
| BD |
又BC=2，BD=8，
∴AB2=2×8=16，∴AB=4．
故答案为：4．
点评：本题考查圆与圆的位置关系及其判定，难点在于圆的弦切角定理的应用，从而利用两三角形相似解决问题，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目