题目内容
下列命题中
①若| •
• |=|
|=| |•|
|•| |,则
|,则 ∥
∥ ;
;
② =(-1,1)在
=(-1,1)在 =(3,4)方向上的投影为
=(3,4)方向上的投影为 ;
;
③若△ABC中,a=5,b=8,c=7则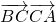 =20;
=20;
④若非零向量 、
、 满足|
满足| +
+ |=
|= ,则|2
,则|2 |>|
|>| +2
+2 |.
|.
其中真命题是________.
①②
分析:选项A根据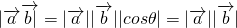 ,则cosθ=±1,θ=0°或180°,则
,则cosθ=±1,θ=0°或180°,则 ∥
∥ 可得结论;
可得结论;
选项B根据投影的定义,应用公式 在
在  方向上的投影为|
方向上的投影为| |cos<
|cos< ,
, >=
>= 求解;
求解;
选项C由余弦定理可知cosC= ,
,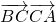 =5×8×cos(π-C)=-20,可知真假;
=5×8×cos(π-C)=-20,可知真假;
对于选项D,显然不正确.
解答:对于选项A,根据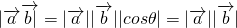 ,则cosθ=±1,θ=0°或180°,则
,则cosθ=±1,θ=0°或180°,则 ∥
∥ ,故正确;
,故正确;
对于选项B,根据投影的定义可得, 在
在  方向上的投影为|
方向上的投影为| |cos<
|cos< ,
, >=
>= =
=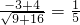 ,故正确;
,故正确;
对于选项C,由余弦定理可知cosC= ,
,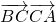 =5×8×cos(π-C)=-20,故不正确;
=5×8×cos(π-C)=-20,故不正确;
对于选项D,| +
+ |=
|= ,不正确;
,不正确;
故答案为:①②
点评:本题主要考查向量的夹角、模以及向量投影的定义及求解的方法等有关知识,解答关键在于要求熟练应用公式,属于中档题.
分析:选项A根据
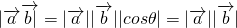 ,则cosθ=±1,θ=0°或180°,则
,则cosθ=±1,θ=0°或180°,则 ∥
∥ 可得结论;
可得结论;选项B根据投影的定义,应用公式
 在
在  方向上的投影为|
方向上的投影为| |cos<
|cos< ,
, >=
>= 求解;
求解;选项C由余弦定理可知cosC=
 ,
,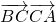 =5×8×cos(π-C)=-20,可知真假;
=5×8×cos(π-C)=-20,可知真假;对于选项D,显然不正确.
解答:对于选项A,根据
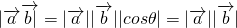 ,则cosθ=±1,θ=0°或180°,则
,则cosθ=±1,θ=0°或180°,则 ∥
∥ ,故正确;
,故正确;对于选项B,根据投影的定义可得,
 在
在  方向上的投影为|
方向上的投影为| |cos<
|cos< ,
, >=
>= =
=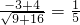 ,故正确;
,故正确;对于选项C,由余弦定理可知cosC=
 ,
,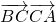 =5×8×cos(π-C)=-20,故不正确;
=5×8×cos(π-C)=-20,故不正确;对于选项D,|
 +
+ |=
|= ,不正确;
,不正确;故答案为:①②
点评:本题主要考查向量的夹角、模以及向量投影的定义及求解的方法等有关知识,解答关键在于要求熟练应用公式,属于中档题.

练习册系列答案
相关题目