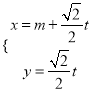Question

【题目】经市场调查，某城市的一种小商品在过去的近20天内的销售量（件）与价格（元）均为时间t（天）的函数，且销售量近似满足g（t）=80﹣2t（件），价格近似满足于 （元）．
（1）试写出该种商品的日销售额y与时间t（0≤t≤20）的函数表达式；
（2）求该种商品的日销售额y的最大值与最小值．

Answer 1

【答案】
（1）解：由已知，由价格乘以销售量可得：

（2）解：由（1）知①当0≤t≤10时y=﹣t2+10t+1200=﹣（t﹣5）2+1225

函数图象开口向下，对称轴为t=5，该函数在t∈[0，5]递增，在t∈（5，10]递减

∴ymax=1225（当t=5时取得），ymin=1200（当t=0或10时取得）

②当10＜t≤20时y=t2﹣90t+2000=（t﹣45）2﹣25

图象开口向上，对称轴为t=45，该函数在t∈（10，20]递减，t=10时，y=1200，ymin=600（当t=20时取得）

由①②知ymax=1225（当t=5时取得），ymin=600（当t=20时取得）

【解析】（1）由已知，由价格乘以销售量可得该种商品的日销售额y与时间t（0≤t≤20）的函数表达式；（2）由（Ⅰ）分段求出函数的最大值与最小值，从而可得该种商品的日销售额y的最大值与最小值．