题目内容
设点O是直角坐标系的原点,点M在直线l:x=-p(p>0)上移动,动点N在线段MO的延长线上,且满点|MN|=|MO|·|NO|.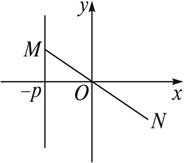
(1)求动点N的轨迹方程;
(2)当p=1时,求|MN|的最小值.
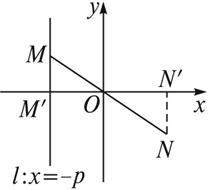
解:(1)过N作NN′垂直x轴于N′,设直线l与x轴交于M′.
设N(x,y)(x>0),则N′(x,0),M′(-p,0),
∵M、O、N三点共线,
∴![]()
由![]()
∵x>0,p>0,将上式整理化简为
(p2-1)x2+p2y2-2px-p2=0(x>0).
(2)当p=1时,N点轨迹为y2=2x+1(x>0),
设N(x,y),M(-1,t).
由M、O、N共线,
得![]() ∴M(-1,-
∴M(-1,-![]() ).
).
则|MN|=![]()
![]()
=x+![]() +2≥2+2=4.
+2≥2+2=4.
当且仅当x=![]() ,即x=1时,等式成立.
,即x=1时,等式成立.
∴当x=1时,|MN|最小值为4.
绿色通道:
本题关键在于能否建立合理的等式,再将等式转化为用动点坐标(x,y)来表示,即可求得动点的轨迹方程.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


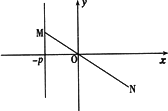
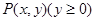 为平面直角坐标系
为平面直角坐标系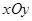 中的一个动点(其中O为坐标原点),点P到定点
中的一个动点(其中O为坐标原点),点P到定点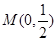 的距离比点P到
的距离比点P到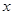 轴的距离大
轴的距离大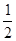 .
. 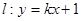 与点P的轨迹相交于A、B两点,且
与点P的轨迹相交于A、B两点,且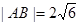 ,求
,求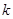 的值.
的值.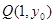 是曲线C上的一点,求以Q为切点的曲线C 的切线方程.
是曲线C上的一点,求以Q为切点的曲线C 的切线方程.