题目内容
(2011•宁德模拟)选修4-4:坐标系与参数方程
在直角坐标xoy中,曲线C的参数方程为
(t为参数),若圆P在以该直角坐标系的原点O为极点、x轴的正半轴为极轴的极坐标系下的方程为ρ2-4ρcos+3=0
(Ⅰ)求曲线C的普通方程和圆P的直角坐标方程;
(Ⅱ)设点A是曲线C上的动点,点B是圆P上的动点,求|AB|的最小值.
在直角坐标xoy中,曲线C的参数方程为
|
(Ⅰ)求曲线C的普通方程和圆P的直角坐标方程;
(Ⅱ)设点A是曲线C上的动点,点B是圆P上的动点,求|AB|的最小值.
分析:(Ⅰ)由参数方程直接求出曲线C的普通方程和利用极坐标方程直接转化为圆P的直角坐标方程;
(Ⅱ)设点A是曲线C上的动点,点B是圆P上的动点,求|AB|的最小值可转化为求|PA|的最小值.
求|AB|的最小值.
(Ⅱ)设点A是曲线C上的动点,点B是圆P上的动点,求|AB|的最小值可转化为求|PA|的最小值.
求|AB|的最小值.
解答: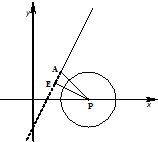
解:(Ⅰ)曲线C
,消去参数t后,解得它的直角坐标方程为2x-y-1=0(x≥1),
因为ρ2=x2+y2,ρcosθ=x,所以ρ2-4ρcosθ+3=0的直角坐标方程为(x-2)2+y2=1.…(4分)
(Ⅱ)过圆心P作射线2x-y-1=0(x≥1)的垂线,垂足E在该射线的反向延长线上,
当点A在射线的端点时,|PA|=
=
,
此时|EA|的长最小,故此时|PA|取最小值.
所以所求的最短距离为
-1.…(7分)

解:(Ⅰ)曲线C
|
因为ρ2=x2+y2,ρcosθ=x,所以ρ2-4ρcosθ+3=0的直角坐标方程为(x-2)2+y2=1.…(4分)
(Ⅱ)过圆心P作射线2x-y-1=0(x≥1)的垂线,垂足E在该射线的反向延长线上,
当点A在射线的端点时,|PA|=
| (2-1)2+(0-1)2 |
| 2 |
此时|EA|的长最小,故此时|PA|取最小值.
所以所求的最短距离为
| 2 |
点评:本题主要考查直线和圆的参数方程及极坐标方程等基础知识,考查运算求解能力及化归与转化思想.

练习册系列答案
相关题目
