题目内容
 (2002•上海)如图所示,客轮以速度2v由A至B再到C匀速航行,货轮从AC的中点D出发,以速度v沿直线匀速航行,将货物送达客轮.已知AB=BC=50海里,若两船同时起航出发,则两船相遇之处距C点
(2002•上海)如图所示,客轮以速度2v由A至B再到C匀速航行,货轮从AC的中点D出发,以速度v沿直线匀速航行,将货物送达客轮.已知AB=BC=50海里,若两船同时起航出发,则两船相遇之处距C点40.8
40.8
海里.(结果精确到小数点后1位)分析:设货轮从出发到两船相遇共航行了x海里,过D点作DF⊥CB于F,连接DE,则DE=x,AB+BE=2x,根据D点是AC的中点,得DF=
AB=100,EF=400-100-2x,在Rt△DFE中,DE2=DF2+EF2,得x2=1002+(300-2x)2解方程求解即可.
| 1 |
| 2 |
解答:解:设货轮从出发到两船相遇共航行了x海里,过D点作DF⊥CB于F,连接DE,则DE=x,AB+BE=2x,
∵D点是AC的中点,
∴DF=
AB=25,EF=50-25-2x,
在Rt△DFE中,DE2=DF2+EF2,得x2=252+(75-2x)2,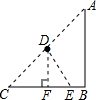
解得x=200±
,
∵200+
>100
(舍去),
∴DE=200-
.
答:货轮从出发到两船相遇共航行了(200-
)海里.
∵D点是AC的中点,
∴DF=
| 1 |
| 2 |
在Rt△DFE中,DE2=DF2+EF2,得x2=252+(75-2x)2,

解得x=200±
100
| ||
| 3 |
∵200+
100
| ||
| 3 |
| 2 |
∴DE=200-
100
| ||
| 3 |
答:货轮从出发到两船相遇共航行了(200-
100
| ||
| 3 |
点评:当三角形中有中点时,常作三角形的中位线.要熟练掌握勾股定理并能利用它作为相等关系列方程求解.

练习册系列答案
相关题目
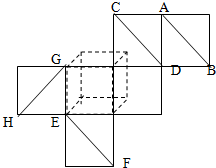 (2002•上海)如图是表示一个正方体表面的一种平面展开图,图中的四条线段AB、CD、EF和GH在原正方体中相互异面的有
(2002•上海)如图是表示一个正方体表面的一种平面展开图,图中的四条线段AB、CD、EF和GH在原正方体中相互异面的有 (2002•上海)如图,三棱柱OAB-O1A1B1,平面OBB1O1⊥平面OAB,∠O1OB=60°,∠AOB=90°,且OB=OO1=2,OA=
(2002•上海)如图,三棱柱OAB-O1A1B1,平面OBB1O1⊥平面OAB,∠O1OB=60°,∠AOB=90°,且OB=OO1=2,OA=