题目内容
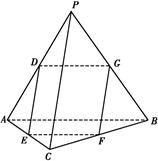
如图,在侧棱垂直底面的四棱柱ABCD A1B1C1D1中,AD∥BC,AD⊥AB,AB=
A1B1C1D1中,AD∥BC,AD⊥AB,AB= ,AD=2,BC=4,AA1=2,E是DD1的中点,F是平面B1C1E与直线AA1的交点.
,AD=2,BC=4,AA1=2,E是DD1的中点,F是平面B1C1E与直线AA1的交点.

(1)证明:①EF∥A1D1;②BA1⊥平面B1C1EF.
(2)求BC1与平面B1C1EF所成的角的正弦值.
 A1B1C1D1中,AD∥BC,AD⊥AB,AB=
A1B1C1D1中,AD∥BC,AD⊥AB,AB= ,AD=2,BC=4,AA1=2,E是DD1的中点,F是平面B1C1E与直线AA1的交点.
,AD=2,BC=4,AA1=2,E是DD1的中点,F是平面B1C1E与直线AA1的交点.
(1)证明:①EF∥A1D1;②BA1⊥平面B1C1EF.
(2)求BC1与平面B1C1EF所成的角的正弦值.
(1)见解析 (2)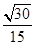
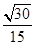
(1)证明:①因为C1B1∥A1D1,C1B1?平面ADD1A1,
所以C1B1∥平面A1D1DA.
又因为平面B1C1EF∩平面A1D1DA=EF,
所以C1B1∥EF,所以A1D1∥EF.
②因为BB1⊥平面A1B1C1D1,所以BB1⊥B1C1.
又因为B1C1⊥B1A1,所以B1C1⊥平面ABB1A1,
所以B1C1⊥BA1.
在矩形ABB1A1中,F是AA1的中点,
tan∠A1B1F=tan∠AA1B=
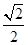 ,
,即∠A1B1F=∠AA1B,
故BA1⊥B1F.
所以BA1⊥平面B1C1EF.
(2)解:设BA1与B1F交点为H,连接C1H.
由(1)知BA1⊥平面B1C1EF,
所以∠BC1H是BC1与平面B1C1EF所成的角.
在矩形AA1B1B中,AB=
 ,AA1=2,得BH=
,AA1=2,得BH= .
.在Rt△BHC1中,BC1=2
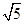 ,BH=
,BH= ,得
,得sin∠BC1H=
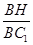 =
=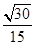 .
.所以BC1与平面B1C1EF所成角的正弦值是
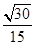 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 平面ABCD,E,F分别为MA,DC的中点,求证:
平面ABCD,E,F分别为MA,DC的中点,求证:

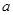 表示直线,
表示直线,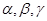 表示不同的平面,则下列命题中正确的是
表示不同的平面,则下列命题中正确的是 且
且 ,则
,则
 且
且 ,则
,则
 且
且 ,则
,则 ,则
,则
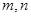 是两条不同的直线,
是两条不同的直线,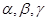 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题: ,则
,则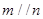 ;②若
;②若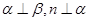 ,则
,则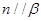 ;
;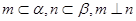 ,则
,则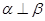 ; ④若
; ④若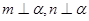 ,则
,则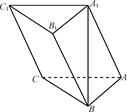
 .
. α
α PQ
PQ α”改成文字叙述是________.
α”改成文字叙述是________.