题目内容
已知椭圆 的右焦点为F,Q、P分别为椭圆上和椭圆外一点,且点Q分FP的比为1:2,则点P的轨迹方程为
的右焦点为F,Q、P分别为椭圆上和椭圆外一点,且点Q分FP的比为1:2,则点P的轨迹方程为
- A.
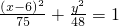
- B.
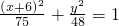
- C.
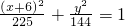
- D.
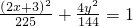
C
分析:根据椭圆的性质可得F的坐标,设Q(x',y'),p(x,y)点Q分FP的比为1:2得y'= y,x'-3=
y,x'-3=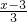 即x'=
即x'=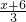 ,代入椭圆方程整理后即可得到答案.
,代入椭圆方程整理后即可得到答案.
解答:设Q(x',y'),p(x,y);则F(3,0) 由点Q分FP的比为1:2得,
y'= y,x'-3=
y,x'-3=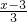 即x'=
即x'=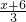 又因为Q在圆上,
又因为Q在圆上,
因此:[(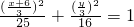 即
即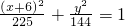
故选C.
点评:本题主要考查轨迹方程的问题.常需要先设出所求点的坐标(x,y),通过题设条件找到x和y的关系.
分析:根据椭圆的性质可得F的坐标,设Q(x',y'),p(x,y)点Q分FP的比为1:2得y'=
 y,x'-3=
y,x'-3=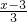 即x'=
即x'=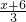 ,代入椭圆方程整理后即可得到答案.
,代入椭圆方程整理后即可得到答案.解答:设Q(x',y'),p(x,y);则F(3,0) 由点Q分FP的比为1:2得,
y'=
 y,x'-3=
y,x'-3=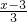 即x'=
即x'=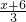 又因为Q在圆上,
又因为Q在圆上,因此:[(
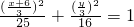 即
即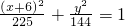
故选C.
点评:本题主要考查轨迹方程的问题.常需要先设出所求点的坐标(x,y),通过题设条件找到x和y的关系.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目

 的右焦点为F,过F的直线(非x轴)交椭圆于M、N两点,右准线
的右焦点为F,过F的直线(非x轴)交椭圆于M、N两点,右准线 交x轴于点K,左顶点为A.
交x轴于点K,左顶点为A.  ,试用
,试用 的右焦点为F,上顶点为A,P为C
的右焦点为F,上顶点为A,P为C 上任一点,MN是圆
上任一点,MN是圆 的一条直径,若与AF平行且在y轴上的截距为
的一条直径,若与AF平行且在y轴上的截距为 的直线
的直线 恰好与圆
恰好与圆 相切.
相切. 的离心率;
的离心率; 的最大值为49,求椭圆C
的最大值为49,求椭圆C