题目内容
当k取什么值时,不等式2kx2+kx-
<0对一切实数x都成立?( )
| 3 |
| 8 |
分析:分别讨论k=0和k≠0,利用不等式恒成立的性质进行求解.
解答:解:若k=0,则不等式等价为-
<0恒成立.满足条件.
若k≠0,要使不等式2kx2+kx-
<0对一切实数x都成立,
则
,
即
,
∴
,即-3<k<0,
综上:-3<k≤0.
故k的取值范围是(-3,0].
故选:D.
| 3 |
| 8 |
若k≠0,要使不等式2kx2+kx-
| 3 |
| 8 |
则
|
即
|
∴
|
综上:-3<k≤0.
故k的取值范围是(-3,0].
故选:D.
点评:本题主要考查不等式恒成立的应用,利用条件将不等式转化为二次函数,利用二次函数的性质进行判断.

练习册系列答案
相关题目
 对一切实数x都成立?
对一切实数x都成立?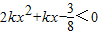 对一切实数x都成立?
对一切实数x都成立?