题目内容
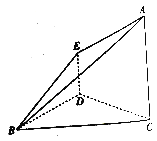
【题目】如图所示,底面为菱形的直四棱柱![]() 被过三点
被过三点![]() 的平面截去一个三棱锥
的平面截去一个三棱锥![]() (图一)得几何体
(图一)得几何体![]() (图二),E为
(图二),E为![]() 的中点.
的中点.
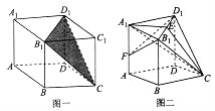
(1)点F为棱![]() 上的动点,试问平面
上的动点,试问平面![]() 与平面
与平面![]() 是否垂直?请说明理由;
是否垂直?请说明理由;
(2)设![]() ,当点F为
,当点F为![]() 中点时,求锐二面角
中点时,求锐二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]()
【解析】
(1)利用直四棱柱的几何特征可知![]() ,
,![]() B1D1⊥平面CEA1,从而平面
B1D1⊥平面CEA1,从而平面![]() 平面CEA1 ;(2) 分别以
平面CEA1 ;(2) 分别以![]() 所在直线为
所在直线为![]() 轴的正方向,建立空间直角坐标系,求出平面
轴的正方向,建立空间直角坐标系,求出平面![]() 与平面F
与平面F![]() 的法向量,代入公式即可得到锐二面角
的法向量,代入公式即可得到锐二面角![]() 的余弦值.
的余弦值.
(1)平面![]() 平面
平面![]() ,证明如下:
,证明如下:
连接AC,BD相交于点O,
因为底面ABCD为菱形,所以AC⊥BD,
又因为直四棱柱上下底面全等,
所以由AC⊥BD得![]() ,
,
又因为CB=CD,![]() ,
,
所以CB1=CD1.
因为E为B1D1的中点,所以![]() ,
,
又![]() ,所以B1D1⊥平面CEA1,
,所以B1D1⊥平面CEA1,
又因为![]() 平面
平面![]() ,
,
所以平面![]() 平面CEA1.
平面CEA1.
(2)连接OE,易知OE⊥平面ABCD,所以OB,OC,OE两两互相垂直,
所以分别以![]() 所在直线为
所在直线为![]() 轴的正方向,建立空间直角坐标系,如图所示,
轴的正方向,建立空间直角坐标系,如图所示,
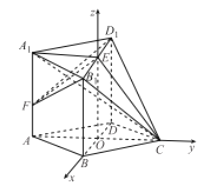
则O(0,0,0),![]() .(7分)
.(7分)
设平面![]() 的法向量为
的法向量为![]() ,则
,则
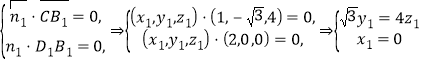 ,
,
令![]()
所以![]() .
.
同理设平面F![]() 的法向量为
的法向量为![]() ,则
,则
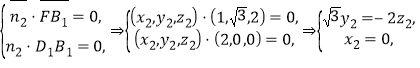 ,
,
令![]() .
.
所以![]() ,
,
所以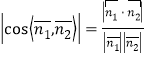
![]() ,
,
所以所求的锐二面角![]() 的余弦值为
的余弦值为![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】假设关于某种设备的使用年限![]() (年)与所支出的维修费用
(年)与所支出的维修费用![]() (万元)有如下统计:
(万元)有如下统计:
| 2 | 3 | 4 | 5 | 6 |
| 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
已知![]() ,
, ![]() .
. 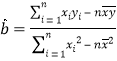 ,
, ![]()
(1)求![]() ,
, ![]() ;
;
(2)![]() 与
与![]() 具有线性相关关系,求出线性回归方程;
具有线性相关关系,求出线性回归方程;
(3)估计使用年限为10年时,维修费用约是多少?