题目内容
三角形ABC的顶点A(1,7),B(-4,2),重心G(
,
).
(1)求三角形ABC的面积;
(2)求三角形ABC外接圆的方程.
| 2 |
| 3 |
| 14 |
| 3 |
(1)求三角形ABC的面积;
(2)求三角形ABC外接圆的方程.
分析:(1)由三角形的重心坐标公式,列式算出点C坐标为(5,5),从而得到向量
、
的坐标,利用三角形面积公式即可算出三角形ABC的面积;
(2)设经过A、B、C三点的圆的方程为x2+y2+Dx+Ey+F=0,代入A、B、C的坐标可得关于D、E、F的方程组,解出D、E、F的值,即可得到△ABC外接圆的方程.
| AC |
| AB |
(2)设经过A、B、C三点的圆的方程为x2+y2+Dx+Ey+F=0,代入A、B、C的坐标可得关于D、E、F的方程组,解出D、E、F的值,即可得到△ABC外接圆的方程.
解答:解:(1)∵A(1,7),B(-4,2),重心G(
,
).
∴设C的坐标为(m,n),由重心坐标公式可得
(1-4+m)=
,
(7+2+n)=
,解之得m=n=5,得点C(5,5),
∴
=(-5,-5),
=(4,-2),
因此,三角形ABC的面积为S=
|(-5)×(-2)-(-5)×4|=15
(2)设三角形ABC外接圆为x2+y2+Dx+Ey+F=0,代入A、B、C三点的坐标,
得
,解之得
,
∴三角形ABC的外接圆方程为x2+y2-2x-4y-20=0.
| 2 |
| 3 |
| 14 |
| 3 |
∴设C的坐标为(m,n),由重心坐标公式可得
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 14 |
| 3 |
∴
| AB |
| AC |
因此,三角形ABC的面积为S=
| 1 |
| 2 |
(2)设三角形ABC外接圆为x2+y2+Dx+Ey+F=0,代入A、B、C三点的坐标,
得
|
|
∴三角形ABC的外接圆方程为x2+y2-2x-4y-20=0.
点评:本题给出三角形的两个顶点和重心坐标,求三角形的面积并求外接圆的方程.着重考查了三角形的重心坐标公式、三角形面积公式和圆的一般方程等知识,属于基础题.

练习册系列答案
相关题目
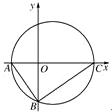 如图,直角三角形ABC的顶点A的坐标为(-2,0),直角顶点B的坐标为(0,-2
如图,直角三角形ABC的顶点A的坐标为(-2,0),直角顶点B的坐标为(0,-2 如图,直角三角形ABC的顶点A的坐标为(-1,0),直角顶点B的坐标为
如图,直角三角形ABC的顶点A的坐标为(-1,0),直角顶点B的坐标为