题目内容
已知三角形ABC的顶点A(-7,0)、B(2,-3)、C(5,6).判断此三角形形状,并求其面积.
分析:由题意可得|AB|=3
,|BC|=3
,|AC|=6
,可得△ABC为等腰直角三角形.再根据三角形的面积为 S△ABC=
|AB|•|BC|,运算求得结果.
| 10 |
| 10 |
| 5 |
| 1 |
| 2 |
解答:解:由题意可得三角形ABC的顶点A(-7,0)、B(2,-3)、C(5,6),
∴|AB|=
=3
,|BC|=
=3
,|AC|=
=6
,
∴|AB|=|BC|,且|AB|2+|BC|2=|AC|2 ,∴△ABC为等腰直角三角形.
∴三角形的面积为 S△ABC=
|AB|•|BC|=
•3
•3
=45.
∴|AB|=
| (2+7)2+(-3-0)2 |
| 10 |
| (5-2)2+(6+3)2 |
| 10 |
| (5+7)2+(6-0)2 |
| 5 |
∴|AB|=|BC|,且|AB|2+|BC|2=|AC|2 ,∴△ABC为等腰直角三角形.
∴三角形的面积为 S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 10 |
| 10 |
点评:本题主要考查两点间的距离公式的应用,通过三角形的三边之长判断三角形的形状,属于中档题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
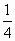 ,
,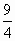 )、B(3,1),C(-1,-3),则∠A的平分线所在直线方程为________.
)、B(3,1),C(-1,-3),则∠A的平分线所在直线方程为________.