题目内容

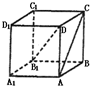精英家教网在正方体A1B1C1D1-ABCD中，AC与B1D所成的角的大小为（　　）
A、
π
6
B、
π
4
C、
π
3
D、
π
2
分析：求异面直线所成角，应平移两条异面直线中的一条或两条，使其成为相交直线，而相交直线所成角，就为异面直线所成角，再放入三角形中，利用解三角形，解出此角即可．
解答：解：可在原图基础上，再向下加一个正方体ABB1A1-MNPQ．在连接B1Q，DQ，则∠DB1Q为所求异面直线所成角或其补角．
cos∠DB1Q=
|DB1|2+|QB1|2-|DQ|2
2|DB1||QB1|
=
(
3
)2+(
2)
2-(
6
)2
2×
3×
2
=0
所以，∠DB1Q=90°，即AC与B1D所成的角的大小为90°．
故选D
点评：本题考查了异面直线所成角的求法，关键在于如何平移．
练习册系列答案
相关题目
精英家教网（甲）如图，已知斜三棱柱ABC-A1B1C1的侧面A1C⊥底面ABC，∠ABC=90°，BC=2，AC=2
3
，又AA1⊥A1C，AA1=A1C．
（1）求侧棱A1A与底面ABC所成的角的大小；
（2）求侧面A1B与底面所成二面角的大小；
（3）求点C到侧面A1B的距离．
（乙）在棱长为a的正方体OABC-O'A'B'C'中，E，F分别是棱AB，BC上的动点，且AE=BF．
（1）求证：A'F⊥C'E；
（2）当三棱锥B'-BEF的体积取得最大值时，求二面角B'-EF-B的大小（结果用反三角函数表示）．
在棱长为a的正方体ABCD-A1B1C1D1中，长度为b（b为定值且b＜a）的线段EF在面对角线A1C1上滑动，G是棱BB1上的动点（G不与端点B1、B重合），下列四个判断：
①三棱柱ABC-A1B1C1的表面积是正方体ABCD-A1B1C1D1表面积的一半；
②三棱锥B1-DEF的体积不变；
③三棱锥G-ADD1的体积等于三棱锥B-A1AD1的体积；
④正方体ABCD-A1B1C1D1外接球的表面积是3πa2．
其中正确命题的个数是（　　）
在棱长为a的正方体ABCD－A1B1C1 D1中，，在面ABCD中取一点F，使 最小，则最小值为       .
在棱长为a的正方体ABCD-A1B1C1D1中，长度为b（b为定值且b＜a）的线段EF在面对角线A1C1上滑动，G是棱BB1上的动点（G不与端点B1、B重合），下列四个判断：
①三棱柱ABC-A1B1C1的表面积是正方体ABCD-A1B1C1D1表面积的一半；
②三棱锥B1-DEF的体积不变；
③三棱锥G-ADD1的体积等于三棱锥B-A1AD1的体积；
④正方体ABCD-A1B1C1D1外接球的表面积是3πa2．
其中正确命题的个数是（ ）
A．4个
B．3个
C．2个
D．1个
（甲）如图，已知斜三棱柱ABC-A1B1C1的侧面A1C⊥底面ABC，∠ABC=90°，BC=2，AC=，又AA1⊥A1C，AA1=A1C．
（1）求侧棱A1A与底面ABC所成的角的大小；
（2）求侧面A1B与底面所成二面角的大小；
（3）求点C到侧面A1B的距离．
（乙）在棱长为a的正方体OABC-O'A'B'C'中，E，F分别是棱AB，BC上的动点，且AE=BF．
（1）求证：A'F⊥C'E；
（2）当三棱锥B'-BEF的体积取得最大值时，求二面角B'-EF-B的大小（结果用反三角函数表示）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网