题目内容
设实数集R为全集,A={x|0≤2x-1≤5},B={x|x2+a<0}.
(1)当a=-4时,求A∩B及A∪B;
(2)若B∩(?RA)=B,求实数a的取值范围.
(1)当a=-4时,求A∩B及A∪B;
(2)若B∩(?RA)=B,求实数a的取值范围.
分析:(1)当a=-4时,根据集合的基本运算即可求A∩B及A∪B;
(2)根据条件B∩(?RA)=B,得到B⊆CRA,然后建立条件方程即可求实数a的取值范围.
(2)根据条件B∩(?RA)=B,得到B⊆CRA,然后建立条件方程即可求实数a的取值范围.
解答:解:(1)已知A={x|
≤x≤
}…(1分)
当a=-4时,B={x|x2-4<0}={x|-2<x<2}…(2分)
∴A∩B={x|
≤x<2}…(4分)
A∪B={x|-2<x≤
}…(6分)
(2)由(1)可知CRA={x|x<
或x>
}…(7分)
由B∩(CRA)=B,
即B⊆CRA…(8分)
当B=φ时,即a≥0时成立 …(9分)
当B≠φ,即a<0时,
则B={x|-
<x<
}…(10分)
则
≤
,
解得0>a≥-
…(11分)
综上a的取值范围是:a≥-
…(12分)
| 1 |
| 2 |
| 5 |
| 2 |
当a=-4时,B={x|x2-4<0}={x|-2<x<2}…(2分)
∴A∩B={x|
| 1 |
| 2 |
A∪B={x|-2<x≤
| 5 |
| 2 |
(2)由(1)可知CRA={x|x<
| 1 |
| 2 |
| 5 |
| 2 |
由B∩(CRA)=B,
即B⊆CRA…(8分)
当B=φ时,即a≥0时成立 …(9分)
当B≠φ,即a<0时,
则B={x|-
| -a |
| -a |
则
| -a |
| 1 |
| 2 |
解得0>a≥-
| 1 |
| 4 |
综上a的取值范围是:a≥-
| 1 |
| 4 |
点评:本题主要考查集合的基本运算,要求熟练掌握集合的交并补运算,比较基础.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
 设实数集R为全集,集合M={x|2≤x≤5},N={x|1<x<3},则图中的阴影部分所表示的集合为( )
设实数集R为全集,集合M={x|2≤x≤5},N={x|1<x<3},则图中的阴影部分所表示的集合为( )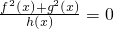 的解集是
的解集是