题目内容
设实数集R为全集，集合P={x|f（x）=0}，Q={x|g（x）=0}，H={x|h（x）=0}，则方程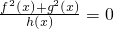
的解集是
- A.P∩Q∩CRH
- B.P∩Q
- C.P∩Q∩H
- D.P∩Q∪H
A
分析：方程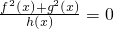等价于：
，方程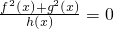的解集是P∩Q∩CRH．
解答：方程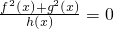等价于：
，
又因为P={x|f（x）=0}，Q={x|g（x）=0}，H={x|h（x）=0}，
所以方程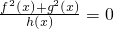的解集是P∩Q∩CRH，
故选A．
点评：本题考查方程的等价转化及交、并、补集的定义，属于基础题．
分析：方程
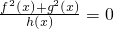等价于：，方程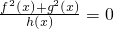的解集是P∩Q∩CRH．解答：方程
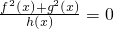等价于：，又因为P={x|f（x）=0}，Q={x|g（x）=0}，H={x|h（x）=0}，
所以方程
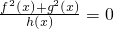的解集是P∩Q∩CRH，故选A．
点评：本题考查方程的等价转化及交、并、补集的定义，属于基础题．
练习册系列答案
相关题目
设实数集R为全集，集合M={x|2≤x≤5}，N={x|1＜x＜3}，则图中的阴影部分所表示的集合为（ ）