Question

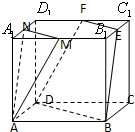如图，正方体ABCD-A₁B₁C₁D₁中，M，N，E，F分别是棱A₁B₁，A₁D₁，B₁C₁，C₁D₁的中点．
（1）求证：直线MN∥平面EFDB；
（2）求证：平面AMN∥平面EFDB．

Answer 1

分析：（1）连结B₁D₁，证明MN∥EF，即可证明直线MN∥平面EFDB； 
（2）证明AM∥平面EFDB，由（1）知MN∥平面EFDB，即可证明平面AMN∥平面EFDB．

解答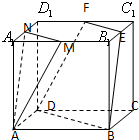：证明：（1）连结B₁D₁                    （1分）
∵M，N，E，F分别是棱A₁B₁，A₁D₁，B₁C₁，C₁D₁的中点
∴MN∥B₁D₁，EF∥B₁D₁                （3分）
∴MN∥EF                                   （4分）
∴直线MN∥平面EFDB；                           （6分）
（2）连MF，
∵ABCD-A₁B₁C₁D₁是正方体         （7分）
∴MF∥A₁D₁且MF=A₁D₁                  （9分）
又A₁D₁=AD且A₁D₁∥AD  
∴MF∥AD且MF=AD    （10分）
∴MFDA是平行四边形                        （11分）
∴AM∥DF                                （12分）
∴AM∥平面EFDB                         （13分）
由（1）知MN∥平面EFDB
∵MN∩AM=M
∴平面AMN∥平面EFDB．                 （14分）

点评：本题考查线面平行，面面平行，考查学生分析解决问题的能力，属于中档题．