题目内容
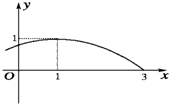 (2007•广州二模)函数f(x)=sin(ωx+?),(x∈R,ω>0,0≤?<2π)的部分图象如图所示,则ω=
(2007•广州二模)函数f(x)=sin(ωx+?),(x∈R,ω>0,0≤?<2π)的部分图象如图所示,则ω=| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
分析:根据函数的图象求出函数的周期,然后求出φ,利用(1,1)求出φ即可.
解答:解:由函数的图象可知,T=4×(3-1)=8,
所以φ=
=
;
因为函数图象过( 1,1),
所以1=sin(
×1+φ),0≤φ<2π,
所以φ=
故答案为:
;
.
所以φ=
| 2π |
| 8 |
| π |
| 4 |
因为函数图象过( 1,1),
所以1=sin(
| π |
| 4 |
所以φ=
| π |
| 4 |
故答案为:
| π |
| 4 |
| π |
| 4 |
点评:本题是基础题,考查三角函数的图象及其性质,三角函数的周期的求法,考查计算能力,常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

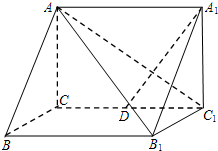 (2007•广州二模)如图所示,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AB=2,BC=1,
(2007•广州二模)如图所示,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AB=2,BC=1,