题目内容
(2007•广州二模)已知曲线C:y=ex(其中e为自然对数的底数)在点P(1,e)处的切线与x轴交于点Q1,过点Q1作x轴的垂线交曲线C于点P1,曲线C在点P1处的切线与x轴交于点Q2,过点Q2作x轴的垂线交曲线C于点P2,…,依次下去得到一系列点P1、P2…、Pn,设点Pn的坐标为(xn,yn)(n∈N*).
(Ⅰ)分别求xn与yn的表达式;
(Ⅱ)设O为坐标原点,求
O
.
(Ⅰ)分别求xn与yn的表达式;
(Ⅱ)设O为坐标原点,求
| n |
 |
| i=1 |
| P | 2 i |
分析:(I)利用导数的几何意义,求曲线C:y=ex在点P(1,e)处的切线方程,依题意即可得P1的坐标为(0,1),同样可求曲线C:y=ex在点Pn(xn,yn)处的切线方程,从而得点Qn+1的横坐标为xn+1=xn-1.数列{xn}是以0为首项,-1为公差的等差数列,利用等差数列的通项公式即可得xn的表达式,进而得yn的表达式;(II)先求出{|OPn|2}的通项公式,再利用拆项求和和等比数列的前n项和公式求和即可
解答:解:(Ⅰ)∵y′=ex,
∴曲线C:y=ex在点P(1,e)处的切线方程为y-e=e(x-1),即y=ex.
此切线与x轴的交点Q1的坐标为(0,0),
∴点P1的坐标为(0,1).
∵点Pn的坐标为(xn,yn)(n∈N*).
∴曲线C:y=ex在点Pn(xn,yn)处的切线方程为y-exn=exn(x-xn)
令y=0,得点Qn+1的横坐标为xn+1=xn-1.
∴数列{xn}是以0为首项,-1为公差的等差数列.
∴xn=1-n,yn=e1-n(n∈N*).
(Ⅱ)∵|OPi|2=xi2+yi2=(i-1)2+e2(1-i)
∴
O
=|OP1|2+|OP2|2+|OP3|2+…+|OPn|2
=(02+e0)+(12+e-2)+=(22+e-4)+…+(n-1)2+e2(1-n)
=[12+22+…+(n-1)2]+[1+e-2+e-4+…+e2(1-n)]
=
+
=
+
∴曲线C:y=ex在点P(1,e)处的切线方程为y-e=e(x-1),即y=ex.
此切线与x轴的交点Q1的坐标为(0,0),
∴点P1的坐标为(0,1).
∵点Pn的坐标为(xn,yn)(n∈N*).
∴曲线C:y=ex在点Pn(xn,yn)处的切线方程为y-exn=exn(x-xn)
令y=0,得点Qn+1的横坐标为xn+1=xn-1.
∴数列{xn}是以0为首项,-1为公差的等差数列.
∴xn=1-n,yn=e1-n(n∈N*).
(Ⅱ)∵|OPi|2=xi2+yi2=(i-1)2+e2(1-i)
∴
| n |
 |
| i=1 |
| P | 2 i |
=(02+e0)+(12+e-2)+=(22+e-4)+…+(n-1)2+e2(1-n)
=[12+22+…+(n-1)2]+[1+e-2+e-4+…+e2(1-n)]
=
| n(n-1)(2n-1) |
| 6 |
| 1-e-2n |
| 1-e-2 |
=
| n(n-1)(2n-1) |
| 6 |
| e2n-1 |
| e2n-2(e2-1) |
点评:本题主要考查数列、导数等基础知识,考查有限与无限的数学思想与方法,以及抽象概括能力、运算求解能力和创新意识,本题解答中用到了高中数学不常用的结论12+22+…+(n-1)2=
,此公式没有必要记忆,高考时基本不涉及
| n(n-1)(2n-1) |
| 6 |

练习册系列答案
相关题目
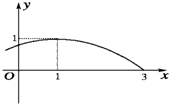 (2007•广州二模)函数f(x)=sin(ωx+?),(x∈R,ω>0,0≤?<2π)的部分图象如图所示,则ω=
(2007•广州二模)函数f(x)=sin(ωx+?),(x∈R,ω>0,0≤?<2π)的部分图象如图所示,则ω=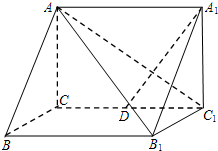 (2007•广州二模)如图所示,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AB=2,BC=1,
(2007•广州二模)如图所示,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AB=2,BC=1,