题目内容

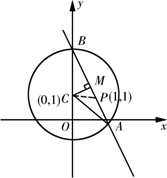
已知圆C：x2＋(y－1)2＝5，直线l：mx－y＋1－m＝0．

(Ⅰ)求证：当m∈R时，直线l与圆C恒有两个不同的交点；

(Ⅱ)设l与圆交于A、B两点，若，求l的倾斜角；

(Ⅲ)求弦AB的中点M的轨迹方程，并说明其轨迹是什么曲线．

答案：
解析：

　　解法一：

　　(Ⅰ)直线l：y－1＝m(x－1)过定点P(1，1)　(1分)

　　而P(1，1)在圆x2＋(y－1)2＝5内部(∵12＋(1－1)2＝1＜5)

　　故当m∈R时，直线l与该圆恒有两个不同的交点．　(4分)

　　(Ⅱ)如图，作CM⊥AB于M，连CA．

　　

　　


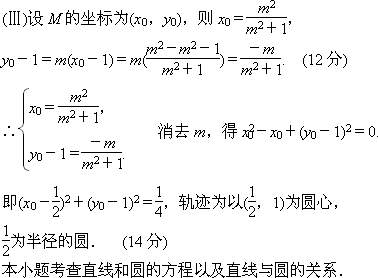
练习册系列答案
相关题目
已知圆C：x2+（y-1）2=5，直线l：mx-y+1-m=0
（1）求证：直线l恒过定点；
（2）设l与圆交于A、B两点，若|AB|=
17
，求直线l的方程．
已知圆C：x2+（y-3）2=4，一动直线l过A （-1，O）与圆C相交于P、Q两点，M是PQ中点，l与直线x+3y+6=0相交于N，则|AM|•|AN|=
 
．
已知圆C：x2+（y-2）2=1
（1）求与圆C相切且在坐标轴上截距相等的直线方程；
（2）和圆C外切且和直线y=1相切的动圆圆心轨迹方程．
已知圆C：x2+（y-1）2=5，直线l：mx-y+1-m=0，
（1）求证对m∈R，直线l和圆C总相交；
（2）设直线l和圆C交于A、B两点，当|AB|取得最大值时，求直线l的方程．
已知圆C：x2+（y-1）2=5，直线l：mx-y+1-m=0
（1）求证：对m∈R，直线l与C总有两个不同的交点；
（2）设l与C交于A、B两点，若|AB|=
17
，求l的方程；
（3）设l与C交于A、B两点且kOA+kOB=2，求直线l的方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网