Question

已知圆C：x²+（y-3）²=4，一动直线l过A （-1，O）与圆C相交于P、Q两点，M是PQ中点，l与直线x+3y+6=0相交于N，则|AM|•|AN|=

 

．

Answer 1

分析：设连接CA并延长交直线x+3y+6=0相交于G，可得CG⊥NG，由垂径定理得CM⊥PQ，可得△AGN∽△AMC，将比例线段转化为等积式，得|AM|•|AN|=|AC|•|AG|=5

解答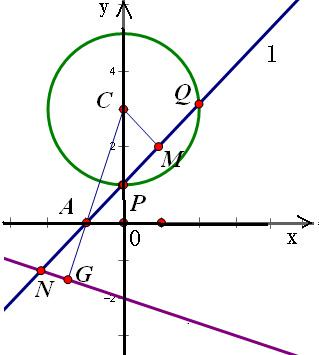：解：设连接CA并延长交直线x+3y+6=0相交于G，连接CM
可得AC的斜率为kAC=

3-0

0+1

=3
∵直线x+3y+6=0的斜率为K1=-

1

3

，kAC•k1=3 ×(-

1

3

) =-1
∴直线AC与直线x+3y+6=0垂直
又∵圆C中，M为弦PQ的中点
∴CM⊥PQ
因此△AGN∽△AMC，可得

|AC|

|AN|

=

|AM|

|AG|

∴|AM|•|AN|=|AC|•|AG|
又∵|AC|=

(-1-0)2+(3-0)2

=

10

|AG|=

|-1+3×0+6|

10

=

10

2

∴|AC|•|AG|=

10

•

10

2

=5
故答案为5

点评：本题考查了直线与圆相交的性质，属于中档题，利用垂径定理得到三角形相似是解决本题的关键．