题目内容
已知函数f(x)=x2+ax+2ln(x-1),a是常数.
(1)证明曲线y=f(x)在点(2,f(2))的切线经过y轴上一个定点;
(2)若f′(x)>(a-3)x2对?x∈(2,3)恒成立,求a的取值范围;
(参考公式:3x3-x2-2x+2=(x+1)(3x2-4x+2))
(3)讨论函数f(x)的单调区间.
解:(1)f(2)=2a+4,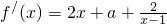 ,…(1分) f′(2)=6+a…(2分),
,…(1分) f′(2)=6+a…(2分),
曲线y=f(x)在点(2,f(2))的切线为y-(2a+4)=(6+a)(x-2)…(3分),
当x=0时,由切线方程得y=-8,所以切线经过y轴上的定点(0,-8)…(4分).
(2)由f′(x)>(a-3)x2得
 …(5分),
…(5分),
对?x∈(2,3),x2-1>0,
所以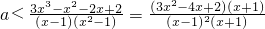
=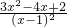 …(6分),
…(6分),
设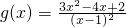 ,则
,则 …(7分)
…(7分)
g(x)在区间(2,3)单调递减…(8分),
所以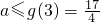 ,a的取值范围为
,a的取值范围为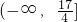 …(9分).
…(9分).
(3)函数f(x)=x2+ax+2ln(x-1)的定义域为(1,+∞),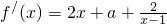
=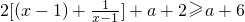 …(10分).
…(10分).
若a≥-6,则f′(x)≥0,f(x)在定义域(1,+∞)上单调增加…(11分);
若a<-6,解方程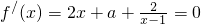 得
得
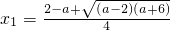 ,
,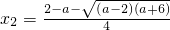 …(12分),
…(12分),
x1>x2>1,当x>x1或1<x<x2时,f′(x)>0;
当x2<x<x1时,f′(x)<0…(13分),
所以f(x)的单调增区间是(1,x2)和(x1,+∞),
单调减区间是[x2,x1](区间无论包含端点x1、x2均可,但要前后一致)…(14分)
分析:(1)先根据题意求出切点与函数的导数,再结合导数的几何意义求出切线的斜率,进而求出切线的方程.
(2)先把问题转化为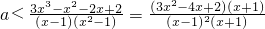 恒成立,然后求出不等式右边的最小值即可求出实数a的取值范围;
恒成立,然后求出不等式右边的最小值即可求出实数a的取值范围;
(3)在函数 的定义域内解不等式fˊ(x)>0和fˊ(x)<0,确定 的单调区间.若在函数式中含字母系数,往往要分类讨论.
点评:本题主要考查函数恒成立问题以及转化思想的应用和计算能力,属于对知识和思想方法的综合考查,属于中档题.对于第三问要注意到参数的取值范围对导数的符号有影响故需要对参数分类讨论,而第二问中关键是把函数是减函数的性质转化为函数恒成立的问题,转化思想在高中数学在应用很广泛.
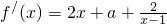 ,…(1分) f′(2)=6+a…(2分),
,…(1分) f′(2)=6+a…(2分),曲线y=f(x)在点(2,f(2))的切线为y-(2a+4)=(6+a)(x-2)…(3分),
当x=0时,由切线方程得y=-8,所以切线经过y轴上的定点(0,-8)…(4分).
(2)由f′(x)>(a-3)x2得
 …(5分),
…(5分),对?x∈(2,3),x2-1>0,
所以
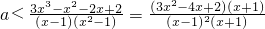
=
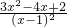 …(6分),
…(6分),设
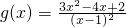 ,则
,则 …(7分)
…(7分)g(x)在区间(2,3)单调递减…(8分),
所以
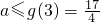 ,a的取值范围为
,a的取值范围为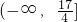 …(9分).
…(9分).(3)函数f(x)=x2+ax+2ln(x-1)的定义域为(1,+∞),
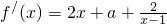
=
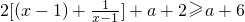 …(10分).
…(10分).若a≥-6,则f′(x)≥0,f(x)在定义域(1,+∞)上单调增加…(11分);
若a<-6,解方程
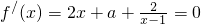 得
得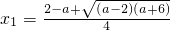 ,
,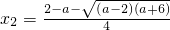 …(12分),
…(12分),x1>x2>1,当x>x1或1<x<x2时,f′(x)>0;
当x2<x<x1时,f′(x)<0…(13分),
所以f(x)的单调增区间是(1,x2)和(x1,+∞),
单调减区间是[x2,x1](区间无论包含端点x1、x2均可,但要前后一致)…(14分)
分析:(1)先根据题意求出切点与函数的导数,再结合导数的几何意义求出切线的斜率,进而求出切线的方程.
(2)先把问题转化为
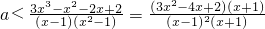 恒成立,然后求出不等式右边的最小值即可求出实数a的取值范围;
恒成立,然后求出不等式右边的最小值即可求出实数a的取值范围;(3)在函数 的定义域内解不等式fˊ(x)>0和fˊ(x)<0,确定 的单调区间.若在函数式中含字母系数,往往要分类讨论.
点评:本题主要考查函数恒成立问题以及转化思想的应用和计算能力,属于对知识和思想方法的综合考查,属于中档题.对于第三问要注意到参数的取值范围对导数的符号有影响故需要对参数分类讨论,而第二问中关键是把函数是减函数的性质转化为函数恒成立的问题,转化思想在高中数学在应用很广泛.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|