题目内容
【题目】如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,四边形ABCD是菱形,AC=2,BD=2 ![]() ,E是PB上任意一点.
,E是PB上任意一点. 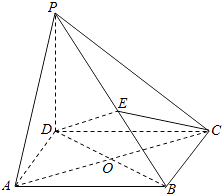
(1)求证:AC⊥DE;
(2)已知二面角A﹣PB﹣D的余弦值为 ![]() ,若E为PB的中点,求EC与平面PAB所成角的正弦值.
,若E为PB的中点,求EC与平面PAB所成角的正弦值.
【答案】
(1)证明:∵PD⊥平面ABCD,AC平面ABCD
∴PD⊥AC
又∵ABCD是菱形,∴BD⊥AC,BD∩PD=D
∴AC⊥平面PBD,∵DE平面PBD
∴AC⊥DE…(6分)
(2)解:分别以OA,OB,OE方向为x,y,z轴建立空间直角坐标系,设PD=t,则 ![]()
由(1)知:平面PBD的法向量为 ![]() ,
,
令平面PAB的法向量为 ![]() ,则根据
,则根据  得
得 ![]() ∴
∴ ![]()
因为二面角A﹣PB﹣D的余弦值为 ![]() ,则
,则 ![]() ,即
,即  ,∴
,∴ ![]()
∴ ![]()
设EC与平面PAB所成的角为θ,
∵ ![]() ,
, ![]()
∴ ![]()

【解析】(1)证明线线垂直,正弦证明线面垂直,即证AC⊥平面PBD;(2)分别以OA,OB,OE方向为x,y,z轴建立空间直角坐标系,设PD=t,用坐标表示点,求得平面PBD的法向量为 ![]() ,平面PAB的法向量为
,平面PAB的法向量为 ![]() ,根据二面角A﹣PB﹣D的余弦值为
,根据二面角A﹣PB﹣D的余弦值为 ![]() ,可求t的值,从而可得P的坐标,再利用向量的夹角公式,即可求得EC与平面PAB所成的角.
,可求t的值,从而可得P的坐标,再利用向量的夹角公式,即可求得EC与平面PAB所成的角.
【考点精析】解答此题的关键在于理解空间中直线与直线之间的位置关系的相关知识,掌握相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点,以及对空间角的异面直线所成的角的理解,了解已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则 .
.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案【题目】“奶茶妹妹”对某时间段的奶茶销售量及其价格进行调查,统计出售价x元和销售量y杯之间的一组数据如下表所示:
价格x | 5 | 5.5 | 6.5 | 7 |
销售量y | 12 | 10 | 6 | 4 |
通过分析,发现销售量y对奶茶的价格x具有线性相关关系.
(Ⅰ)求销售量y对奶茶的价格x的回归直线方程;
(Ⅱ)欲使销售量为13杯,则价格应定为多少?
注:在回归直线y= ![]() 中,
中, 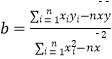 ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
. ![]() =146.5.
=146.5.