题目内容
直线y=2x是△ABC中∠C的平分线所在直线,若A(-4,2),B(3,1)(1)求点A关于y=2x对称点E的坐标;
(2)求点C的坐标;
(3)求△ABC的面积.
【答案】分析:(1)设点A关于y=2x对称点E的坐标为E(a,b),则y=2x是线段AE的垂直平分线,由此能求出点E坐标.
(2)设C(x,2x)由直线y=2x是三角形ABC中∠C的平分线所在直线,知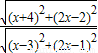 =
=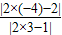 ,由此能求出C点坐标.
,由此能求出C点坐标.
(3)由A(-4,2),B(3,1),C(2,4),利用斜率公式能得到△ABC是以∠C为直角的直角三角形,再用平面向量公式分别求出|AC|和|BC|,由此能求出△ABC的面积.
解答:解:(1)设点A关于y=2x对称点E的坐标为E(a,b),
则y=2x是线段AE的垂直平分线,
∵A(-4,2),
∴设直线AB的方程为:y-2=- (x+4),即x+2y=0,
(x+4),即x+2y=0,
解方程组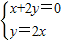 ,得AE的中点坐标为(0,0),
,得AE的中点坐标为(0,0),
∴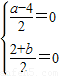 ,解得a=4,b=-2,∴E(4,-2).
,解得a=4,b=-2,∴E(4,-2).
(2)设C(x,2x)
∵直线y=2x是三角形ABC中∠C的平分线所在直线,
∴ =
=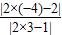 ,
,
整理,得3x2-8x+4=0,
解得x= ,或x=2.
,或x=2.
经验证x= 不能构成三角形,所以x=2,
不能构成三角形,所以x=2,
故C点坐标为:C(2,4).
(3)∵A(-4,2),B(3,1),C(2,4),
∴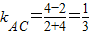 ,kBC=
,kBC=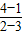 =-3,
=-3,
∴kAC•kBC=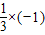 =-1,
=-1,
∴△ABC是以∠C为直角的直角三角形,
∵|AC|=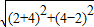 =2
=2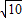 ,
,
|BC|=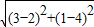 =
=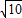 ,
,
∴△ABC的面积=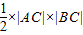 =
=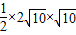 =10.
=10.
点评:本题考查点的坐标的求法,考查三角形面积的求法,具体涉及到直线方程、中点坐标公式、点到直线的距离、两点间距离、向量等基本知识点,解题时要认真审题,仔细解答,注意等价转化思想的合理运用.
(2)设C(x,2x)由直线y=2x是三角形ABC中∠C的平分线所在直线,知
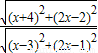 =
=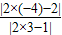 ,由此能求出C点坐标.
,由此能求出C点坐标.(3)由A(-4,2),B(3,1),C(2,4),利用斜率公式能得到△ABC是以∠C为直角的直角三角形,再用平面向量公式分别求出|AC|和|BC|,由此能求出△ABC的面积.
解答:解:(1)设点A关于y=2x对称点E的坐标为E(a,b),
则y=2x是线段AE的垂直平分线,
∵A(-4,2),
∴设直线AB的方程为:y-2=-
 (x+4),即x+2y=0,
(x+4),即x+2y=0,解方程组
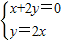 ,得AE的中点坐标为(0,0),
,得AE的中点坐标为(0,0),∴
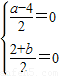 ,解得a=4,b=-2,∴E(4,-2).
,解得a=4,b=-2,∴E(4,-2).(2)设C(x,2x)
∵直线y=2x是三角形ABC中∠C的平分线所在直线,
∴
 =
=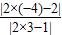 ,
,整理,得3x2-8x+4=0,
解得x=
 ,或x=2.
,或x=2.经验证x=
 不能构成三角形,所以x=2,
不能构成三角形,所以x=2,故C点坐标为:C(2,4).
(3)∵A(-4,2),B(3,1),C(2,4),
∴
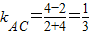 ,kBC=
,kBC=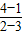 =-3,
=-3,∴kAC•kBC=
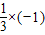 =-1,
=-1,∴△ABC是以∠C为直角的直角三角形,
∵|AC|=
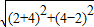 =2
=2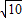 ,
,|BC|=
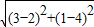 =
=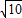 ,
,∴△ABC的面积=
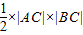 =
=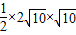 =10.
=10.点评:本题考查点的坐标的求法,考查三角形面积的求法,具体涉及到直线方程、中点坐标公式、点到直线的距离、两点间距离、向量等基本知识点,解题时要认真审题,仔细解答,注意等价转化思想的合理运用.

练习册系列答案
相关题目