题目内容
 如图,椭圆C:
如图,椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
F2,|A1B1|=
| 7 |
S?A1B1A2B 2=2S?B1F1B2F 2
(1)求椭圆C的方程;
(2)设l是过原点的直线,直线n与l垂直相交于P点,且n与椭圆相交于A,B两点,|OP|=1,求
| AP |
| PB |
分析:(1)由|A1B1|=
,知a2+b2=7,由SA1B1A2 B2=2SB1F1B2F2,知a=2c,由此能求出椭圆C的方程.
(2)设A(x1,y1),B(x2,y2),当直线n的斜率不存在时,由对称性取P(1,0),A(1,
),B(1,-
),则
•
=
.当直线n的斜率存在时,令AB:y=kx+m,由|OP|=1,知m2=1+k2,
•
=(
-
)•(
-
)=1-
•
.联立
,得(3+4k2)x2+8kmx+4m2-12=0,再利用韦达定理进行运算能够求出
•
的取值范围.
| 7 |
(2)设A(x1,y1),B(x2,y2),当直线n的斜率不存在时,由对称性取P(1,0),A(1,
| 3 |
| 2 |
| 3 |
| 2 |
| AP |
| PB |
| 9 |
| 2 |
| AP |
| PB |
| OP |
| OA |
| OB |
| OP |
| OA |
| OB |
|
| AP |
| PB |
解答:解:(1)由|A1B1|=
,知a2+b2=7,①
由SA1B1A2 B2=2SB1F1B2F2,知a=2c,②
又b2=a2-c2,③
由①②③解得a2=4,b2=3,故椭圆C的方程为
+
=1.
(2)设A(x1,y1),B(x2,y2),
当直线n的斜率不存在时,由对称性取P(1,0),A(1,
),B(1,-
),
则
•
=
.
当直线n的斜率存在时,令AB:y=kx+m,
∵|OP|=1,∴
=1,即m2=1+k2,
∵|OP|=1,∴
•
=(
-
)•(
-
)=1-
•
.
联立
,得(3+4k2)x2+8kmx+4m2-12=0,
∴
,(*)
∴
•
=(1+k2)x1x2+km(x1+x2)+m2,
将(*)代入并化简得
•
=
,
∴
•
=1+
,
由1+k2=m2,得m2≥1,∴0<
≤1,∴
<
•
≤
,
综上所述,
•
的取值范围是(
,
].
| 7 |
由SA1B1A2 B2=2SB1F1B2F2,知a=2c,②
又b2=a2-c2,③
由①②③解得a2=4,b2=3,故椭圆C的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)设A(x1,y1),B(x2,y2),
当直线n的斜率不存在时,由对称性取P(1,0),A(1,
| 3 |
| 2 |
| 3 |
| 2 |
则
| AP |
| PB |
| 9 |
| 2 |
当直线n的斜率存在时,令AB:y=kx+m,
∵|OP|=1,∴
| |m| | ||
|
∵|OP|=1,∴
| AP |
| PB |
| OP |
| OA |
| OB |
| OP |
| OA |
| OB |
联立
|
∴
|
∴
| OA |
| OB |
将(*)代入并化简得
| OA |
| OB |
| -5m2 |
| 4m2-1 |
∴
| AP |
| PB |
| 5 | ||
4-
|
由1+k2=m2,得m2≥1,∴0<
| 1 |
| m2 |
| 9 |
| 4 |
| AP |
| PB |
| 8 |
| 3 |
综上所述,
| AP |
| PB |
| 9 |
| 4 |
| 8 |
| 3 |
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆、向量的相关知识,解题时要注意合理地进行等价转化.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
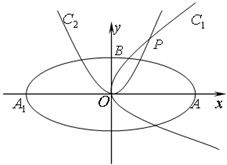 如图,椭圆C:
如图,椭圆C: (2008•闸北区二模)如图,椭圆C:
(2008•闸北区二模)如图,椭圆C: 如图,椭圆
如图,椭圆 (2011•重庆三模)光线被曲线反射,等效于被曲线在反射点处的切线反射.已知光线从椭圆的一个焦点出发,被椭圆反射后要回到椭圆的另一个焦点;光线从双曲线的一个焦点出发被双曲线反射后的反射光线等效于从另一个焦点发出;如图,椭圆C:
(2011•重庆三模)光线被曲线反射,等效于被曲线在反射点处的切线反射.已知光线从椭圆的一个焦点出发,被椭圆反射后要回到椭圆的另一个焦点;光线从双曲线的一个焦点出发被双曲线反射后的反射光线等效于从另一个焦点发出;如图,椭圆C: