题目内容
已知函数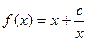 的定义域为
的定义域为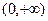 ,若对任意的
,若对任意的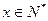 ,都有
,都有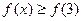 求
求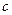 范围
范围
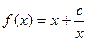 的定义域为
的定义域为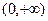 ,若对任意的
,若对任意的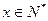 ,都有
,都有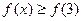 求
求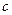 范围
范围9
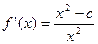
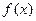 的最小值为
的最小值为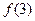 ,故
,故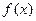 在
在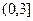 单调减,在
单调减,在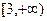 单调增故当
单调增故当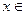
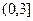 时,
时,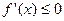 ,
,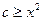 在
在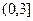 恒成立,所以
恒成立,所以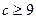
当
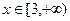 时,
时,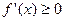 ,
,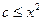 在
在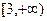 恒成立,所以
恒成立,所以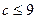 ,又
,又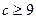 ,故
,故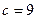
解法二:
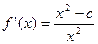 ,由已知
,由已知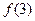 为极小值,故
为极小值,故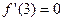 ,即
,即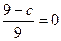 ,
,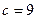
解法三:易知
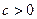 ,且
,且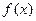 在
在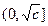 单调减,在
单调减,在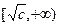 单调增,又由已知
单调增,又由已知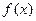 的最小值为
的最小值为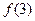 ,故
,故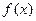 在
在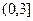 单调减,在
单调减,在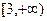 单调,所以
单调,所以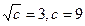

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
题目内容
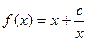 的定义域为
的定义域为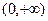 ,若对任意的
,若对任意的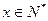 ,都有
,都有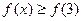 求
求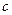 范围
范围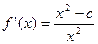
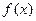 的最小值为
的最小值为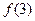 ,故
,故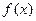 在
在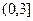 单调减,在
单调减,在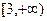 单调增故当
单调增故当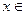
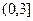 时,
时,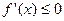 ,
,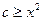 在
在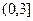 恒成立,所以
恒成立,所以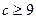
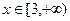 时,
时,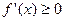 ,
,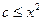 在
在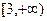 恒成立,所以
恒成立,所以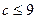 ,又
,又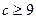 ,故
,故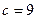
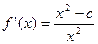 ,由已知
,由已知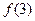 为极小值,故
为极小值,故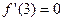 ,即
,即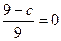 ,
,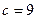
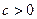 ,且
,且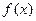 在
在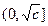 单调减,在
单调减,在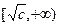 单调增,又由已知
单调增,又由已知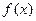 的最小值为
的最小值为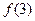 ,故
,故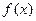 在
在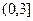 单调减,在
单调减,在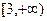 单调,所以
单调,所以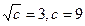

 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案