题目内容
19.已知函数f(x)=$\left\{\begin{array}{l}{|lo{g}_{3}x|,0<x<3}\\{sin\frac{π}{3}x,3≤x≤9}\end{array}\right.$,若存在实数a,b,c,d满足a<b<c<d,且f(a)=f(b)=f(c)=f(d),则$\frac{(c-3)(d-3)}{ab}$的取值范围是(18,20.25).分析 画出函数f(x)的图象,可得ab=1,再由正弦函数的对称性,可得c+d=15,6<c<7.5.由二次函数的值域求法,即可得到所求范围.
解答 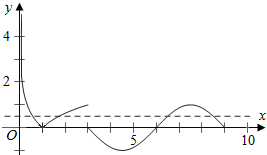 解:画出函数f(x)的图象,
解:画出函数f(x)的图象,
可知|log3a|=|log3b|,
即有-log3a=log3b,即为ab=1,
当x=7.5时,f(x)=sin$\frac{5π}{2}$=1,
即有c+d=15,6<c<7.5.
则$\frac{(c-3)(d-3)}{ab}$=(c-3)(d-3)=(c-3)(12-c)
=-c2+15c-36=-(c-7.5)2+20.25.
即有区间(6,7.5)为增区间,
即有$\frac{(c-3)(d-3)}{ab}$∈(18,20.25).
故答案为:(18,20.25).
点评 本题考查分段函数的应用,考查对数函数和三角函数的图象的运用,同时考查二次函数的性质及正弦函数的对称性,属于中档题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
9.(普通中学做)如图所示,程序框图输出的某一实数对(x,y)中,若y=32,则x=( )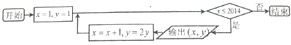
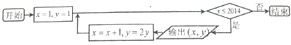
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
4.|sin165°|•cos15°-sin255°•|sin195°|的值是( )
| A. | 0 | B. | -$\frac{1}{2}$ | C. | 1 | D. | $\frac{1}{2}$ |