题目内容
【题目】如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,PA=AB=AD=2,四边形ABCD满足AB⊥AD,BC∥AD且BC=4,点M为PC的中点,点E为BC边上的点,且 ![]() =λ.
=λ. 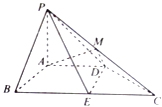
(1)求证:平面ADM⊥平面PBC;
(2)是否存在实数λ,使得二面角P﹣DE﹣B的余弦值为 ![]() ?若存在,求出实数λ的值,若不存在,请说明理由.
?若存在,求出实数λ的值,若不存在,请说明理由.
【答案】
(1)证明:取PB中点N,连结MN,AN,
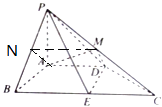
∵M是PC中点,∴MN∥BC,MN= ![]() ,
,
又∵BC∥AD,∴MN∥AD,MN=AD,
∴四边形ADMN为平行四边形,
∵AP⊥AD,AB⊥AD,∴AD⊥平面PAB,
∴AD⊥AN,∴AN⊥MN,
∵AP=AB,∴AN⊥PB,∴AN⊥平面PBC,
∵AN平面ADM,∴平面ADM⊥平面PBC.
(2)解:存在实数λ=1,使得二面角P﹣DE﹣B的余弦值为 ![]() .
.
∵λ=1,∴点E为BC边的中点,
∴DE∥AB,∴DE⊥平面PAD,
∴∠PDA为二面角P﹣DE﹣B的一个平面角,
在等腰Rt△PDA中,∠PDA= ![]() ,
,
∴二面角P﹣DE﹣B的余弦值为 ![]() .
.
【解析】(1)取PB中点N,连结MN,AN,推导出四边形ADMN为平行四边形,由AP⊥AD,AB⊥AD,得AD⊥AN,AN⊥MN,由此能证明平面ADM⊥平面PBC.(2)λ=1时,点E为BC边的中点,∠PDA为二面角P﹣DE﹣B的一个平面角,由此推导出二面角P﹣DE﹣B的余弦值为 ![]() .
.
【考点精析】本题主要考查了平面与平面垂直的判定的相关知识点,需要掌握一个平面过另一个平面的垂线,则这两个平面垂直才能正确解答此题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


