题目内容
(本小题满分12分)已知函数y=f(x)=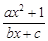 (a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)<
(a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)<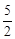 .试求函数f(x)的解析式
.试求函数f(x)的解析式
【答案】
f(x)=x+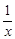 .
.
【解析】本题考查函数的解析式,考查函数的奇偶性,考查利用基本不等式求函数的最值,属于中档题.
根据f(x)是奇函数,可得f(-x)=-f(x),从而可求c=0,f(x)= 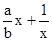 ,利用基本不等式可求最小值,由f(1)<
,利用基本不等式可求最小值,由f(1)< 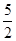 ,即2b2-5b+2<0,可求b=1,a=1,故可求函数的解析式.
,即2b2-5b+2<0,可求b=1,a=1,故可求函数的解析式.
∵f(x)是奇函数,∴f(-x)=-f(x),
即 ∴c=0,
∴c=0,
∵a>0,b>0,x>0,∴f(x)= ≥2
≥2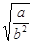 ,
,
当且仅当x=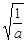 时等号成立,于是2
时等号成立,于是2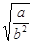 =2,∴a=b2,
=2,∴a=b2,
由f(1)< 得
得 <
< 即
即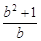 <
< ,
,
∴2b2-5b+2<0,解得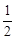 <b<2,
<b<2,
又b∈N,∴b=1,∴a=1,∴f(x)=x+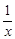 .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目