题目内容
忆知函数f(x)=ln|x|(x≠0),函数g(x)=![]() +
+![]() (x)(x≠0)
(x)(x≠0)
(1)当x≠0时,求函数y=g(x)的表达式;
(2)若a>0,函数y=g(x)在(0,+∞)上的最小值是2,求a的值;
(3)在(2)的条件下,求直线y=![]() x+
x+![]() 与函数y=g(x)的图象所围成图形的面积.
与函数y=g(x)的图象所围成图形的面积.
答案:
解析:
解析:
|
解:(1)∵ ∴当 ∴当 ∴当 (2)∵由(1)知当 ∴当 ∴函数 (3)由 ∴直线 |

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
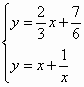 解得
解得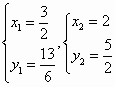
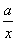 .
.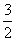 ,求a的值;
,求a的值;