题目内容
(04年全国卷Ⅱ理)(14分)
已知函数f(x)=ln(1+x)-x,g(x)=xlnx.
(1)求函数f(x)的最大值;
(2)设0<a<b,证明:0<g(a)+g(b)-2g(![]() )<(b-a)ln2.
)<(b-a)ln2.
解析:(I)解:函数f(x)的定义域是(-1,∞),![]() (x)=
(x)=![]() .令
.令![]() (x)=0,解得x=0,当-1<x<0时,
(x)=0,解得x=0,当-1<x<0时, ![]() (x)>0,当x>0时,
(x)>0,当x>0时,![]() (x)<0,又f(0)=0,故当且仅当x=0时,f(x)取得最大值,最大值是0
(x)<0,又f(0)=0,故当且仅当x=0时,f(x)取得最大值,最大值是0![]()
(II)证法一:g(a)+g(b)-2g(![]() )=alna+blnb-(a+b)ln
)=alna+blnb-(a+b)ln![]() =a
=a![]() .
.
由(I)的结论知ln(1+x)-x<0(x>-1,且x≠0),由题设0<a<b,得![]() ,因此
,因此![]() ,
,![]() .
.
所以a![]() >-
>-![]() .
.
又![]() a
a![]() <a
<a![]()
综上0<g(a)+g(b)-2g(![]() )<(b-a)ln2.
)<(b-a)ln2.
(II)证法二:g(x)=xlnx,![]() ,设F(x)= g(a)+g(x)-2g(
,设F(x)= g(a)+g(x)-2g(![]() ),
),
则![]() 当0<x<a时
当0<x<a时![]() 因此F(x)在(0,a)内为减函数
因此F(x)在(0,a)内为减函数![]() 当x>a时
当x>a时![]() 因此F(x)在(a,+∞)上为增函数
因此F(x)在(a,+∞)上为增函数![]() 从而,当x=a时,F(x)有极小值F(a)
从而,当x=a时,F(x)有极小值F(a)![]() 因为F(a)=0,b>a,所以F(b)>0,即0<g(a)+g(b)-2g(
因为F(a)=0,b>a,所以F(b)>0,即0<g(a)+g(b)-2g(![]() ).
).
设G(x)=F(x)-(x-a)ln2,则![]() 当x>0时,
当x>0时,![]() ,因此G(x)在(0,+∞)上为减函数,因为G(a)=0,b>a,所以G(b)<0.即g(a)+g(b)-2g(
,因此G(x)在(0,+∞)上为减函数,因为G(a)=0,b>a,所以G(b)<0.即g(a)+g(b)-2g(![]() )<(b-a)ln2.
)<(b-a)ln2.

练习册系列答案
相关题目
 ( )
( ) D.-
D.-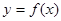 是奇函数,则当
是奇函数,则当 时,
时, ,设
,设 的反函数是
的反函数是 ,则
,则