Question

已知函数f(x)＝ln x－.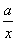

(1)若a>0，试判断f(x)在定义域内的单调性；

(2)若f(x)在[1，e]上的最小值为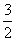，求a的值；

(3)若f(x)<x²在(1，＋∞)上恒成立，求a的取值范围．

 

Answer 1

【答案】

（1）f(x)在(0，＋∞)上是单调递增函数

（2）a＝－.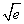

（3）a≥－1时，f(x)<x²在(1，＋∞)上恒成立

【解析】

试题分析：解　(1)由题意f(x)的定义域为(0，＋∞)，且f′(x)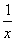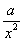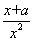＝＋＝.因为a>0，所以f′(x)>0，故f(x)在(0，＋∞)上是单调递增函数．  3分

(2)由(1)可知，f′(x)＝.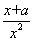

①若a≥－1，则x＋a≥0，即f′(x)≥0在[1，e]上恒成立，此时f(x)在[1，e]上为增函数，

所以f(x)_min＝f(1)＝－a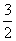＝，所以a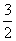＝－ (舍去)．  5分

②若a≤－e，则x＋a≤0，即f′(x)≤0在[1，e]上恒成立，此时f(x)在[1，e]上为减函数，

所以f(x)_min＝f(e)＝1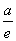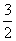－＝?a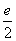＝－ (舍去)．   7分

③若－e<a<－1，令f′(x)＝0得x＝－a，当1<x<－a时，f′(x)<0，所以f(x)在[1，－a]上为减函数；当－a<x<e时，f′(x)>0，所以f(x)在[－a，e]上为增函数，所以f(x)_min＝f(－a)＝ln(－a)＋1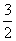＝?a＝－.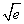 

综上所述，a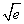＝－.     9分

(3)因为f(x)<x²，所以ln x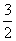－<x².又x>0，所以a>xln x－x³.

令g(x)＝xln x－x³，

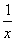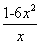h(x)＝g′(x)＝1＋ln x－3x²，h′(x)＝－6x＝.   11分

因为x∈(1，＋∞)时，h′(x)<0，h(x)在(1，＋∞)上是减函数．

所以h(x)<h(1)＝－2<0，即g′(x)<0，

所以g(x)在[1，＋∞)上也是减函数，则g(x)<g(1)＝－1，

所以a≥－1时，f(x)<x²在(1，＋∞)上恒成立．  13分

考点：导数的运用

点评：主要是考查了导数在研究函数中的运用，属于基础题。