题目内容
一个空间几何体的三视图及部分数据如图1所示.
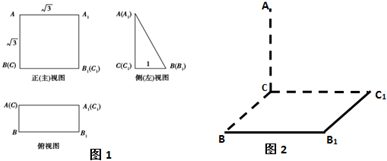
(1)请在图2中补充完整该几何体的直观图,并求它的体积;
(2)证明:A1C⊥平面AB1C1;
(3)若D是棱CC1的中点,在棱AB上取中点E,判断DE是否平行于平面AB1C1,并证明你的结论.

(1)请在图2中补充完整该几何体的直观图,并求它的体积;
(2)证明:A1C⊥平面AB1C1;
(3)若D是棱CC1的中点,在棱AB上取中点E,判断DE是否平行于平面AB1C1,并证明你的结论.
分析:(1)由三视图知几何体为一直三棱柱,高为
,底面三角形为直角三角形,两直角边长分别为
,1,代入棱柱的体积公式计算;
(2)根据线面垂直的判定定理只需证明A1C⊥B1C1;A1C⊥AC1即可;
(3)当E为棱AB的中点时,DE∥平面AB1C1,利用证明平面DEF∥平面AB1C1,可得线面平行.
| 3 |
| 3 |
(2)根据线面垂直的判定定理只需证明A1C⊥B1C1;A1C⊥AC1即可;
(3)当E为棱AB的中点时,DE∥平面AB1C1,利用证明平面DEF∥平面AB1C1,可得线面平行.
解答:解:(1)几何体的直观图如图.
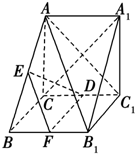
几何体为一直三棱柱,高为
,底面三角形为直角三角形,两直角边长分别为
,1,
∴其体积V=
×1×
×
=
;
(2)证明:∵∠ACB=90°,∴BC⊥AC.
∵三棱柱ABC-A1B1C1为直三棱柱,∴BC⊥CC1.
∵AC∩CC1=C,∴BC⊥平面ACC1A1,∴BC⊥A1C.
∵B1C1∥BC,∴B1C1⊥A1C.
∵四边形ACC1A1为正方形,∴A1C⊥AC1.
∵B1C1∩AC1=C1,
∴A1C⊥平面AB1C1;
(3)当E为棱AB的中点时,
DE∥平面AB1C1.
证明:如图,取BB1的中点F,连结EF,FD,DE,
∵D,E,F分别为CC1,AB,BB1的中点,∴EF∥AB1.
∵AB1?平面AB1C1,EF?平面AB1C1,
∴EF∥平面AB1C1.同理可得FD∥平面AB1C1,
又EF∩FD=F,∴平面DEF∥平面AB1C1.
而DE?平面DEF,∴DE∥平面AB1C1.

几何体为一直三棱柱,高为
| 3 |
| 3 |
∴其体积V=
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| 2 |
(2)证明:∵∠ACB=90°,∴BC⊥AC.
∵三棱柱ABC-A1B1C1为直三棱柱,∴BC⊥CC1.
∵AC∩CC1=C,∴BC⊥平面ACC1A1,∴BC⊥A1C.
∵B1C1∥BC,∴B1C1⊥A1C.
∵四边形ACC1A1为正方形,∴A1C⊥AC1.
∵B1C1∩AC1=C1,
∴A1C⊥平面AB1C1;
(3)当E为棱AB的中点时,
DE∥平面AB1C1.
证明:如图,取BB1的中点F,连结EF,FD,DE,
∵D,E,F分别为CC1,AB,BB1的中点,∴EF∥AB1.
∵AB1?平面AB1C1,EF?平面AB1C1,
∴EF∥平面AB1C1.同理可得FD∥平面AB1C1,
又EF∩FD=F,∴平面DEF∥平面AB1C1.
而DE?平面DEF,∴DE∥平面AB1C1.
点评:本题由三视图求几何体的体积,考查了线面垂直及线面平行的证明,解题的关键是判断三视图的数据所对应的几何量及几何图形的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
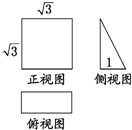 一个空间几何体的三视图及部分数据如图所示,则这个几何体的体积是( )
一个空间几何体的三视图及部分数据如图所示,则这个几何体的体积是( )| A、3 | ||
B、
| ||
| C、2 | ||
D、
|
 一个空间几何体的三视图及部分数据如图所示(单位:cm),则这个几何体的体积是( )
一个空间几何体的三视图及部分数据如图所示(单位:cm),则这个几何体的体积是( )| A、3cm3 | ||
B、
| ||
| C、2cm3 | ||
D、
|

 一个空间几何体的三视图及部分数据如图所示(单位cm),则这个几何体的体积是( )
一个空间几何体的三视图及部分数据如图所示(单位cm),则这个几何体的体积是( ) 一个空间几何体的三视图及部分数据如图所示(单位:cm),则这个几何体的表面积是
一个空间几何体的三视图及部分数据如图所示(单位:cm),则这个几何体的表面积是