题目内容
函数 是定义域为
是定义域为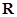 的可导函数,且对任意实数
的可导函数,且对任意实数 都有
都有 成立.若当
成立.若当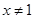 时,不等式
时,不等式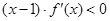 成立,设
成立,设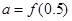 ,
,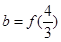 ,
, ,则
,则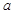 ,
,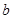 ,
, 的大小关系是( )
的大小关系是( )
A.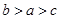 | B.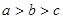 |
C.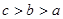 | D.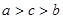 |
A
解析试题分析:由f(x)=f(2-x)可得,函数f(x)的图象关于直线x=1对称,所以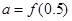 =
= 。再由 (x-1)•f′(x)<0成立可得,当x>1,f′(x)<0,故函数f(x)在(1,+∞)上是减函数;当x<1,f′(x)>0,故函数f(x)在(-∞,1)上是增函数. 因为
。再由 (x-1)•f′(x)<0成立可得,当x>1,f′(x)<0,故函数f(x)在(1,+∞)上是减函数;当x<1,f′(x)>0,故函数f(x)在(-∞,1)上是增函数. 因为 ,所以
,所以 ,即
,即 ,即 b>a>c,故选A.
,即 b>a>c,故选A.
考点:不等关系与不等式;导数的运算.
点评:本题主要考查函数的对称性和单调性的综合应用,不等式与不等关系,属于基础题.函数 对定义域内的任意实数
对定义域内的任意实数 都有
都有 成立,则
成立,则 的对称轴为
的对称轴为 。
。

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
已知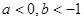 ,则下列不等式成立的是( )
,则下列不等式成立的是( )
A.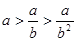 | B.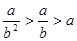 |
C.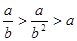 | D.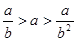 |
已知a,b,c∈R,下列命题中正确的是( )
A.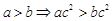 | B.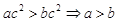 |
C.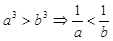 | D.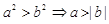 |
设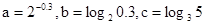 ,则
,则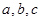 的大小关系是
的大小关系是
A.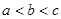 | B.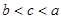 |
C.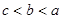 | D.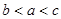 |
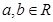 ,下列命题正确的是( )
,下列命题正确的是( )
A.若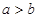 ,则 ,则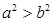 | B.若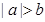 ,则 ,则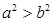 |
C.若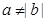 ,则 ,则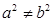 | D.若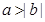 ,则 ,则 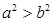 |
已知-1<a+b<3,2<a-b<4,则2a+3b的范围是( )
A.(-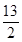 , ,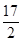 ) ) | B.(-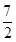 , , ) ) |
C.(-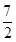 , ,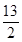 ) ) | D.(-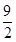 , ,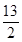 ) ) |
若a、b、c∈R,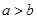 ,则下列不等式成立的是( )
,则下列不等式成立的是( )
A.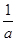 < <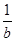 | B. |
C.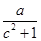 > >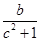 | D. |
已知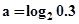 ,
,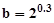 ,
,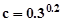 ,则
,则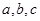 三者的大小关系是 ( )
三者的大小关系是 ( )
A.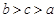 | B.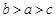 | C.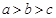 | D.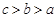 |
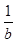 -
-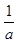 =1,则a-b<1;
=1,则a-b<1;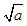 -
-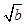 |=1,则|a-b|<1;④若|a3-b3|=1,则|a-b|<1.
|=1,则|a-b|<1;④若|a3-b3|=1,则|a-b|<1.