题目内容
已知![]()
(1)若![]() 存在单调递减区间,求
存在单调递减区间,求![]() 的取值范围;
的取值范围;
(2)若![]() 时,求证
时,求证![]() 成立;
成立;
(3)利用(2)的结论证明:若![]()
解:(1)![]()
![]() ,
,
![]() 有单调减区间
有单调减区间![]() 有解,
有解, ![]()
![]() 有解, ①
有解, ①![]() 时合题意
时合题意
②![]() 时,
时,![]() ,即
,即![]()
![]() 的范围是
的范围是![]()
(2)设![]()
![]()
![]()
|
|
| 0 |
|
|
| + | 0 | - |
|
|
| 最大值 |
|
![]() 有最大值0
有最大值0
![]() 恒成立 即
恒成立 即![]() 成立
成立
(3)![]()
![]()
![]()
![]() 由(2)
由(2)
![]() ,
, ![]() 求证成立
求证成立

练习册系列答案
相关题目

 使得
使得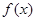 ≥0成立,求
≥0成立,求 的范围
的范围
 >1时,在(1)的条件下,
>1时,在(1)的条件下,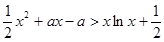 成立
成立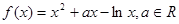
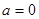 时,求函数
时,求函数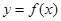 在点
在点 处的切线方程;
处的切线方程; 在
在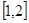 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围;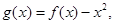 是否存在实数
是否存在实数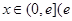 是自然对数的底)时,函数
是自然对数的底)时,函数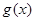 的最小值是3,
的最小值是3,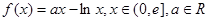
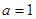 ,求
,求 的极小值;
的极小值; 使
使